
Archetype Definition Language 1.4 (ADL1.4)
| Issuer: openEHR Specification Program | |
|---|---|
Release: AM Release-2.2.0 |
Status: STABLE |
Revision: [latest_issue] |
Date: [latest_issue_date] |
Keywords: EHR, ADL, AOM, health records, archetypes, constraint language, ISO 13606, openehr |
|
| © 2003 - 2022 The openEHR Foundation | |
|---|---|
The openEHR Foundation is an independent, non-profit foundation, facilitating the sharing of health records by consumers and clinicians via open specifications, clinical models and open platform implementations. |
|
Licence |
|
Support |
Issues: Problem Reports |
Amendment Record
| Issue | Details | Raiser, Implementer | Completed |
|---|---|---|---|
AM Release 2.2.0 |
|||
AM Release 2.1.0 |
|||
AM Release 2.0.6 |
|||
SPECAM-24: Standardise structure for recording governance meta-data in 1.4 archetypes. |
S Garde, |
||
Release 1.0.2 |
|||
1.4.1 |
SPEC-268: Correct missing parentheses in dADL type identifiers. dADL grammar and cADL scanner rules updated. |
R Chen |
12 Dec 2008 |
SPEC-284: Correct inconsistencies in naming of |
A Torrisi |
||
SPEC-260: Correct the regex published for the |
P Gummer, |
||
Release 1.0.1 |
|||
1.4.0 |
SPEC-203: Release 1.0 explanatory text improvements. Improve Archetype slot explanation. |
T Beale |
13 Mar 2007 |
SPEC-208: Improve ADL grammar for assertion expressions. |
T Beale |
||
SPEC-160: Duration constraints. Added ISO 8601 patterns for duration in cADL. |
S Heard |
||
SPEC-213: Correct ADL grammar for date/times to be properly ISO 8601-compliant. Include 'T' in cADL patterns and dADL and cADL Date/time, Time and Duration values. |
T Beale |
||
SPEC-216: Allow mixture of W, D etc in ISO 8601 Duration (deviation from standard). |
S Heard |
||
SPEC-200: Correct Release 1.0 typographical errors. |
A Patterson |
||
SPEC-225: Allow generic type names in ADL. |
M Forss |
||
SPEC-226: Rename |
T Beale |
||
SPEC-233: Define semantics for |
K Atalag |
||
SPEC-241: Correct cADL grammar for archeype slot match expressions |
S Heard |
||
SPEC-223: Clarify quoting rules in ADL |
A Patterson |
||
SPEC-242: Allow non-inclusive two-sided ranges in ADL. |
S Heard |
||
SPEC-245: Allow term bindings to paths in archetypes. |
S Heard |
||
Release 1.0 |
|||
1.3.1 |
SPEC-136. Add validity rules to ADL document. |
T Beale |
18 Jan 2006 |
SPEC-171. Add validity check for cardinality & occurrences |
A Maldondo |
||
1.3.0 |
SPEC-141. Allow point intervals in ADL. Updated atomic types part of cADL section and dADL grammar section. |
S Heard |
18 Jun 2005 |
SPEC-142. Update dADL grammar to support assumed values. |
T Beale |
||
Release 0.95 |
|||
1.2.1 |
SPEC-125. |
T Beale |
11 Feb 2005 |
1.2 |
SPEC-110. Update ADL document and create AOM document. |
T Beale |
15 Nov 2004 |
Added explanatory material; added domain type support; rewrote of most dADL sections. Added section on assumed values, "controlled" flag, nested container structures. Change language handling. |
A Rector |
||
Various changes to assertions due to input from the DSTC. |
A Goodchild |
|
|
Detailed review from Clinical Information Project, Australia. |
E Browne |
||
Remove UML models to "Archetype Object Model" document. |
T Beale |
||
Detailed review from CHIME, UCL. |
T Austin |
||
SPEC-103. Redevelop archetype UML model, add new keywords: |
T Beale |
||
SPEC-104. Fix ordering bug when |
K Atalag |
||
Added grammars for all parts of ADL, as well as new UML diagrams. |
T Beale |
||
Release 0.9 |
|||
1.1 |
SPEC-79. Change interval syntax in ADL. |
T Beale |
24 Jan 2004 |
1.0 |
SPEC-77. Add cADL date/time pattern constraints. |
S Heard, |
14 Jan 2004 |
0.9.9 |
SPEC-73. Allow lists of Reals and Integers in cADL. |
T Beale, |
28 Dec 2003 |
0.9.8 |
SPEC-70. Create Archetype System Description. Moved Archetype Identification Section to new Archetype System document. Copyright Assgined by Ocean Informatics P/L Australia to The openEHR Foundation. |
T Beale, |
29 Nov 2003 |
0.9.7 |
Added simple value list continuation (",…"). Changed path syntax so that trailing '/' required for object paths. |
T Beale |
01 Nov 2003 |
0.9.6 |
Additions during HL7 WGM Memphis Sept 2003 |
T Beale |
09 Sep 2003 |
0.9.5 |
Added comparison to other formalisms. Renamed CDL to cADL and dDL to dADL. Changed path syntax to conform (nearly) to Xpath. Numerous small changes. |
T Beale |
03 Sep 2003 |
0.9 |
Rewritten with sections on cADL and dDL. |
T Beale |
28 July 2003 |
0.8.1 |
Added basic type constraints, re-arranged sections. |
T Beale |
15 July 2003 |
0.8 |
Initial Writing |
T Beale |
10 July 2003 |
Acknowledgements
Trademarks
-
'Microsoft' and '.Net' are registered trademarks of the Microsoft Corporation.
-
'Java' is a registered trademark of Oracle Corporation
-
'Linux' is a registered trademark of Linus Torvalds.
-
'openEHR' is a registered trademark of The openEHR Foundation
-
'SNOMED CT' is a registered trademark of IHTSDO
Supporters
The work reported in this paper has been funded by the following organisations:
-
UCL (University College London) - Centre for Health Informatics and Multiprofessional Education (CHIME);
-
Ocean Informatics.
Special thanks to Prof David Ingram, founding Director of CHIME, UCL, who provided a vision and collegial working environment ever since the days of GEHR (1992).
1. Preface
1.1. Purpose
This document describes the design basis and syntax of the Archetype Definition Language 1.4 (ADL 1.4). It is intended for software developers, technically-oriented domain specialists and subject matter experts (SMEs). ADL is designed as an abstract human-readable and computer-processible syntax. ADL archetypes can be hand-edited using a normal text editor.
The intended audience includes:
-
Standards bodies producing health informatics standards;
-
Academic groups using openEHR;
-
The open source healthcare community;
-
Solution vendors;
-
Medical informaticians and clinicians interested in health information.
1.2. Related Documents
Prerequisite documents for reading this document include:
Related documents include:
1.3. Nomenclature
In this document, the term 'attribute' denotes any stored property of a type defined in an object model, including primitive attributes and any kind of relationship such as an association or aggregation. XML 'attributes' are always referred to explicitly as 'XML attributes'.
1.4. Status
This specification is in the STABLE state. The development version of this document can be found at https://specifications.openehr.org/releases/AM/Release-2.2.0/ADL1.4.html.
Known omissions or questions are indicated in the text with a 'to be determined' paragraph, as follows:
TBD: (example To Be Determined paragraph)
|
Note
|
this specification is a re-formatted issue of the original ADL 1.4 Specification from openEHR Release 1.0.2. There are slight changes in formatting, citations and other references, corrections to typographical errors and changed syntax colourisation due to the use of more modern language-based syntax colourisers in the publishing tools. |
|
Note
|
for users requiring the most recent form of ADL and archteype technology in general, the Archetype Definition Language 2 (ADL2) specifications should be used. In particular, the Archetype Technology Overview should be referred to for the most current description of Archetype Technology. |
1.5. Feedback
Feedback may be provided on the openEHR ADL forum.
Issues may be raised on the specifications Problem Report tracker.
To see changes made due to previously reported issues, see the AM component Change Request tracker.
1.6. Conformance
Conformance of a data or software artifact to an openEHR specification is determined by a formal test of that artifact against the relevant openEHR Implementation Technology Specification(s) (ITSs), such as an IDL interface or an XML-schema. Since ITSs are formal derivations from underlying models, ITS conformance indicates model conformance.
1.7. Tools
Various tools exist for creating and processing archetypes. The ADL Workbench is a reference compiler, visualiser and editor. The openEHR tools can be downloaded from the website .
Source projects can be found at the openEHR Github project.
2. Overview
2.1. What is ADL?
Archetype Definition Language (ADL) is a formal language for expressing archetypes, which are constraint-based models of domain entities, or what some might call 'structured business rules'. The archetype concept is described by Beale [Beale_2000], [Beale_2002]. The openEHR Archetype Object Model 1.4 describes the definitive semantic model of archetypes, in the form of an object model. The ADL syntax is one possible serialisation of an archetype.
The openEHR archetype framework is described in terms of Archetype Definitions and Principles and an Archetype System. Other semantic formalisms considered in the course of the development of ADL, and some which remain relevant are described in detailed in Appendix A.
ADL uses three other syntaxes, cADL (constraint form of ADL), dADL (data definition form of ADL), and a version of first-order predicate logic (FOPL), to describe constraints on data which are instances of some information model (e.g. expressed in UML). It is most useful when very generic information models are used for describing the data in a system, for example, where the logical concepts PATIENT, DOCTOR and HOSPITAL might all be represented using a small number of classes such as PARTY and ADDRESS. In such cases, archetypes are used to constrain the valid structures of instances of these generic classes to represent the desired domain concepts. In this way future-proof information systems can be built - relatively simple information models and database schemas can be defined, and archetypes supply the semantic modelling, completely outside the software. ADL can thus be used to write archetypes for any domain where formal object model(s) exist which describe data instances.
When archetypes are used at runtime in particular contexts, they are composed into larger constraint structures, with local or specialist constraints added, via the use of templates. The formalism of templates is dADL. Archetypes can be specialised by creating an archetypes that reference existing archetypes as parents; such archetypes can only make certain changes while remaining compatible with the parent.
Another major function of archetypes is to connect information structures to formal terminologies. Archetypes are language-neutral, and can be authored in and translated into any language.
Finally, archetypes are completely path-addressable in a manner similar to XML data, using path expressions that are directly convertible to Xpath expressions.
2.1.1. Structure
Archetypes expressed in ADL resemble programming language files, and have a defined syntax. ADL itself is a very simple 'glue' syntax, which uses two other syntaxes for expressing structured constraints and data, respectively. The cADL syntax is used to express the archetype definition section, while the ODIN syntax is used to express data which appears in the language, description, terminology, and `revision_history' sections of an ADL archetype. The top-level structure of an ADL archetype is shown in the figure below.
This main part of this document describes cADL and ADL path syntax, before going on to describe the combined ADL syntax, archetypes and domain-specific type libraries.
2.1.2. An Example
The following is an example of a very simple archetype, giving a feel for the syntax. The main point to glean from the following is that the notion of 'guitar' is defined in terms of constraints on a generic model of the concept "INSTRUMENT". The names mentioned down the left-hand side of the definition section (INSTRUMENT, size etc) are alternately class and attribute names from an object model. Each block of braces encloses a specification for some particular set of instances that conform to a specific concept, such as 'guitar' or 'neck', defined in terms of constraints on types from a generic class model. The leaf pairs of braces enclose constraints on primitive types such as Integer, String, Boolean and so on.
archetype (adl_version=1.4)
adl-test-instrument.guitar.draft.v1
concept
[at0000]
language
original_language = <[iso_639-1::en]>
definition
INSTRUMENT[at0000] matches {
size matches {|60..120|} -- size in cm
date_of_manufacture matches {yyyy-mm-??} -- year & month ok
parts cardinality matches {0..*} matches {
PART[at0001] matches { -- neck
material matches {[local::at0003, at0004]} -- timber or nickel alloy
}
PART[at0002] matches { -- body
material matches {[local::at0003]} -- timber
}
}
}
ontology
term_definitions = <
["en"] = <
items = <
["at0000"] = <
text = <"guitar">;
description = <"stringed instrument">
>
["at0001"] = <
text = <"neck">;
description = <"neck of guitar">
>
["at0002"] = <
text = <"body">;
description = <"body of guitar">
>
["at0003"] = <
text = <"timber">;
description = <"straight, seasoned timber">
>
["at0004"] = <
text = <"nickel alloy">;
description = <"frets">
>
>
>
>2.1.3. Semantics
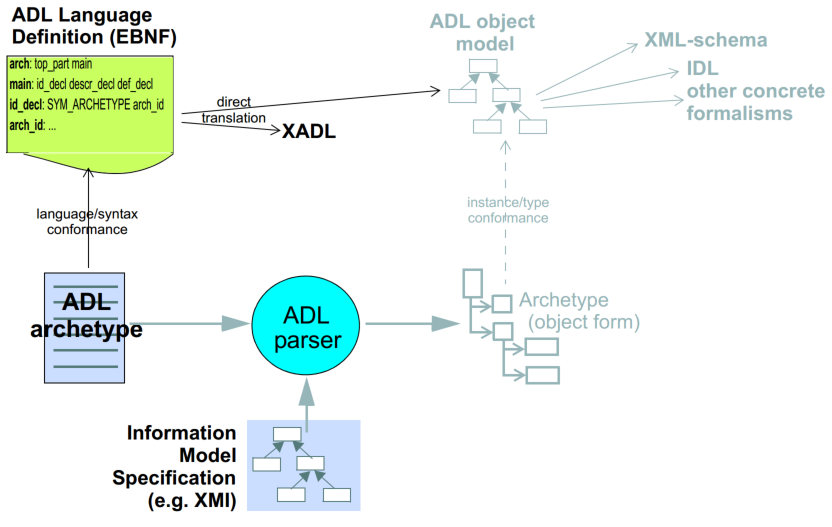
As a parsable syntax, ADL has a formal relationship with structural models such as those expressed in UML, according to the scheme of the following figure. Here we can see that ADL documents are parsed into a network of objects (often known as a ‘parse tree’) which are themselves defined by a formal, abstract object model (see The openEHR Archetype Object Model 1.4. Such a model can in turn be reexpressed as any number of concrete models, such as in a programming language, XML-schema or OMG IDL.
While ADL syntax remains the primary abstract formalism for expressing archetypes, the AOM defines the semantics of an archetype, in particular relationships which must hold true between the parts of an archetype for it to be valid as a whole.
2.2. Computational Context
Archetypes are distinct, structured models of domain content, such as 'data captured for a blood pressure observation'. They sit between lower layers of knowledge resources in a computing environment, such as clinical terminologies and ontologies, and actual data in production systems. Their primary purpose is to provide a reusable, interoperable way of managing generic data so that it conforms to particular structures and semantic constraints. Consequently, they bind terminology and ontology concepts to information model semantics, in order to make statements about what valid data structures look like. ADL provides a solid formalism for expressing, building and using these entities computationally. Every ADL archetype is written with respect to a particular information model, often known as a 'reference model', if it is a shared, public specification.
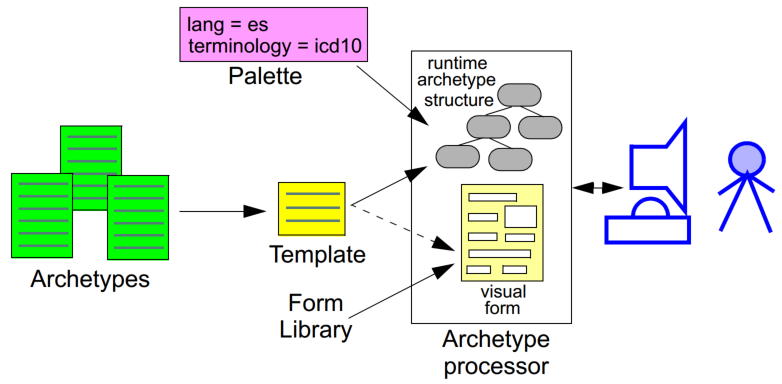
Archetypes are applied to data via the use of templates, which are defined at a local level. Templates generally correspond closely to screen forms, and may be re-usable at a local or regional level. Templates do not introduce any new semantics to archetypes, they simply specify the use of particular archetypes, further compatible constraints, and default data values.
A third artifact governing the functioning of archetypes and templates at runtime is the local palette, which specifies which natural language(s) and terminologies are in use in the locale. The use of a palette removes irrelevant languages and terminology bindings from archetypes, retaining only those relevant to actual use. The following figure illustrates the overall environment in which archetypes, templates, and a locale palette exist.
2.3. XML form of Archetypes
With ADL parsing tools it is possible to convert ADL to any number of forms, including various XML formats. XML instance can be generated from the object form of an archetype in memory. An XML-schema corresponding to the ADL Object Model is published at openEHR.org.
2.4. Changes from Previous Versions
For existing users of ADL or archetype development tools, the following provides a guide to the changes in the syntax.
2.4.1. Version 1.4 from Version 1.3
A number of small changes were made in this version, along with significant tightening up of the explanatory text and examples.
2.4.1.1. ISO 8601 Date/Time Conformance
All ISO 8601 date, time, date/time and duration values in dADL are now conformant (previously the usage of the 'T' separator was not correct). Constraint patterns in cADL for dates, times and date/times are also corrected, with a new constraint pattern for ISO 8601 durations being added. The latter allows a deviation from the standard to include the 'W' specifier, since durations with a mixture of weeks, days etc is often used in medicine.
2.4.1.2. Non-inclusive Two-sided Intervals
It is now possible to define an interval of any ordered amount (integer, real, date, time, date/time, duration) where one or both of the limits is not included, for example:
|0..<1000| -- 0 >= x < 1000
|>0.5..4.0| -- 0.5 > x <= 4.0
|>P2d..<P10d| -- 2 days > x < 10 days2.4.2. Version 1.3 from Version 1.2
The specific changes made in version 1.3 of ADL are as follows.
2.4.2.1. Query syntax replaced by URI data type
In version 1.2 of ADL, it was possible to include an external query, using syntax of the form:
attr_name = <query("some_service", "some_query_string")>This is now replaced by the use of URIs, which can express queries, for example:
attr_name = <http://some.service.org?some%20query%20etc>No assumption is made about the URI; it need not be in the form of a query - it may be any kind of URI.
2.4.2.2. Top-level Invariant Section
In this version, invariants can only be defined in a top level block, in a way similar to object-oriented class definitions, rather than on every block in the definition section, as is the case in version 1.2 of ADL. This simplifies ADL and the Archetype Object Model, and makes an archetype more comprehensible as a type definition.
2.4.3. Version 1.2 from Version 1.1
2.4.3.1. ADL Version
The ADL version is now optionally (for the moment) included in the first line of the archetype, as follows.
archetype (adl_version=1.2)It is strongly recommended that all tool implementors include this information when archetypes are saved, enabling archetypes to gradually become imprinted with their correct version, for more reliable later processing. The adl_version indicator is likely to become mandatory in future versions of ADL.
2.4.3.2. dADL Syntax Changes
The dADL syntax for container attributes has been altered to allow paths and typing to be expressed more clearly, as part of enabling the use of Xpath-style paths. ADL 1.1 dADL had the following appearance:
school_schedule = <
locations(1) = <...>
locations(2) = <...>
locations(3) = <...>
subjects("philosophy:plato") = <...>
subjects("philosophy:kant") = <...>
subjects("art") = <...>
>This has been changed to look like the following:
school_schedule = <
locations = <
[1] = <...>
[2] = <...>
[3] = <...>
>
subjects = <
["philosophy:plato"] = <...>
["philosophy:kant"] = <...>
["art"] = <...>
>
>The new appearance both corresponds more directly to the actual object structure of container types, and has the property that paths can be constructed by directly reading identifiers down the backbone of any subtree in the structure. It also allows the optional addition of typing information anywhere in the structure, as shown in the following example:
school_schedule = SCHEDULE <
locations = LOCATION <
[1] = <...>
[2] = <...>
[3] = ARTS_PAVILLION <...>
>
subjects = <
["philosophy:plato"] = ELECTIVE_SUBJECT <...>
["philosophy:kant"] = ELECTIVE_SUBJECT <...>
["art"] = MANDATORY_SUBJECT <...>
>
>These changes will affect the parsing of container structures and keys in the description and terminology parts of the archetype.
2.4.3.3. Revision History Section
Revision history is now recorded in a separate section of the archetype, both to logically separate it from the archetype descriptive details, and to facilitate automatic processing by version control systems in which archtypes may be stored. This section is included at the end of the archetype because it is in general a monotonically growing section.
2.4.3.4. Primary_language and Languages_available Sections
An attribute previously called primary_language was required in the ontology section of an ADL 1.1 archetype. This is renamed to original_language and is now moved to a new top level section in the archetype called language. Its value is still expressed as a dADL String attribute. The languages_available attribute previously required in the ontology section of the archetype is renamed to translations, no longer includes the original languages, and is also moved to this new top level section.
3. File Encoding and Character Quoting
3.1. File Encoding
Because ADL files are inherently likely to contain multiple languages due to internationalised authoring and translation, they must be capable of accommodating characters from any language. ADL files do not explicitly indicate an encoding because they are assumed to be in UTF-8 encoding of unicode. For ideographic and script-oriented languuages, this is a necessity.
There are three places in ADL files where non-ASCII characters can occur:
-
in string values, demarcated by double quotes, e.g. "xxxx";
-
in regular expression patterns, demarcated by either
//or^^; -
in character values, demarcated by single quotes, e.g. 'x'.
URIs (a data type in ODIN) are assumed to be 'percent-encoded' according to IETF RFC 3986, which applies to all characters outside the 'unreserved set'. The unreserved set is:
unreserved = ALPHA / DIGIT / "-" / "." / "_" / "~"In actual fact, ADL files encoded in latin 1 (ISO-8859-1) or another variant of ISO-8859 - both containing accented characters with unicode codes outside the ASCII 0-127 range - may work perfectly well, for various reasons:
-
the contain nothing but ASCII, i.e. unicode code-points 0 - 127; this will be the case in English- language authored archetypes containing no foreign words;
-
some layer of the operating system is smart enough to do an on-the-fly conversion of characters above 127 into UTF-8, even if the archetype tool being used is designed for pure UTF-8 only;
-
the archetype tool (or the string-processing libraries it uses) might support UTF-8 and ISO- 8859 variants.
For situations where binary UTF-8 (and presumably other UTF-* encodings) cannot be supported, ASCII encoding of unicode characters above code-point 127 should only be done using the system supported by many programming languages today, namely \u escaped UTF-16. In this system, unicode codepoints are mapped to either:
-
\uHHHH- 4 hex digits which will be the same (possibly 0-filled on the left) as the unicode code-point number expressed in hexadecimal; this applies to unicode codepoints in the rangeU+0000-U+FFFF(the 'base multi-lingual plane', BMP); -
\uHHHHHHHH- 8 hex digits to encode unicode code-points in the rangeU+10000throughU+10FFFF(non-BMP planes); the algorithm is described in IETF RFC 2781.
It is not expected that the above approach will be commonly needed, and it may not be needed at all; it is preferable to find ways to ensure that native UTF-8 can be supported, since this reduces the burden for ADL parser and tool implementers. The above guidance is therefore provided only to ensure a standard approach is used for ASCII-encoded unicode, if it becomes unavoidable.
Thus, while the only officially designated encoding for ADL and its constituent syntaxes is UTF-8, real software systems may be more tolerant. This document therefore specifies that any tool designed to process ADL files need only support UTF-8; supporting other encodings is an optional extra. This could change in the future, if required by the ADL or openEHR user community.
3.2. Special Character Sequences
In strings and characters, characters not in the lower ASCII (0-127) range should be UTF-8 encoded, with the exception of quoted single- and double quotes, and some non-printing characters, for which the following customary quoted forms are allowed (but not required):
-
\r- carriage return -
\n- linefeed -
\t- tab -
\\- backslash -
\"- literal double quote -
\'- literal single quote
Any other character combination starting with a backslash is illiegal; to get the effect of a literal backslash, the \\ sequence should always be used.
Typically in a normal string, including multi-line paragraphs as used in ODIN, only \\ and \" are likely to be necessary, since all of the others can be accommodated in their literal forms; the same goes for single characters - only \\ and \' are likely to commonly occur. However, some authors may prefer to use \n and \t to make intended formatting clearer, or to allow for text editors that do not react properly to such characters. Parsers should therefore support the above list.
In regular expressions (only used in cADL string constraints), there will typically be backslashescaped characters from the above list as well as other patterns like \s (whitspace) and \d (decimal digit), according to the PERL regular expression specification ([Perl_regex]). These should not be treated as anything other than literal strings, since they are processed by a regular expression parser.
4. dADL - Data ADL
4.1. Overview
The dADL syntax provides a formal means of expressing instance data based on an underlying object-oriented or relational information model, which is readable both by humans and machines. The general appearance is exemplified by the following:
person = (List<PERSON>) <
[01234] = <
name = < -- person's name
forenames = <"Sherlock">
family_name = <"Holmes">
salutation = <"Mr">
>
address = < -- person's address
habitation_number = <"221B">
street_name = <"Baker St">
city = <"London">
country = <"England">
>
>
[01235] = < -- etc >
>In the above the attribute names person , name , address etc, and the type List<PERSON> are all assumed to come from an information model. The [01234] and [01235] tags identify container items.
The basic design principle of dADL is to be able to represent data in a way that is both machine-processible and human readable, while making the fewest assumptions possible about the information model to which the data conforms. To this end, type names are optional; often, only attribute names and values are explicitly shown. No syntactical assumptions are made about whether the underlying model is relational, object-oriented or what it actually looks like. More than one information model can be compatible with the same dADL-expressed data. The UML semantics of composition/aggregation and association are expressible, as are shared objects. Literal leaf values are only of 'standard' widely recognised types, i.e. Integer, Real, Boolean, String, Character and a range of Date/time types. In standard dADL, all complex types are expressed structurally.
A common question about dADL is why it is needed, when there is already XML? To start with, this question highlights the widespread misconception about XML, namely that because it can be read by a text editor, it is intended for humans. In fact, XML is designed for machine processing, and is textual to guarantee its interoperability. Realistic examples of XML (e.g. XML-schema instance, OWL-RDF ontologies) are generally unreadable for humans. dADL is on the other hand designed as a human-writable and readable formalism that is also machine processable; it may be thought of as an abstract syntax for object-oriented data. dADL also differs from XML by:
-
providing a more comprehensive set of leaf data types, including intervals of numerics and date/time types, and lists of all primitive types;
-
adhering to object-oriented semantics, particularly for container types, which XML schema languages generally do not;
-
not using the confusing XML notion of ‘attributes’ and ‘elements’ to represent what are essentially object properties;
-
requiring half the space of the equivalent XML.
Of course, this does not prevent XML exchange syntaxes being used for dADL, and indeed the conversion to XML instance is rather straighforward. Details on the XML expression of dADL and use of Xpath expressions is described in Section 4.7.
The dADL syntax as described above has a number of useful characteristics that enable the extensive use of paths to navigate it, and express references. These include:
-
each
<>block corresponds to an object (i.e. an instance of some type in an information model); -
the name before an '=' is always an attribute name or else a container element key, which attaches to the attribute of the enclosing block;
-
paths can be formed by navigating down a tree branch and concatenating attribute name, container keys (where they are encountered) and '/' characters;
-
every node is reachable by a path;
-
shared objects can be referred to by path references.
4.2. Basics
4.2.1. Scope of a dADL Document
A dADL document may contain one or more objects from the same object model.
4.2.2. Keywords
dADL has no keywords of its own: all identifiers are assumed to come from an information model.
4.2.3. Reserved Characters
In dADL, a small number of characters are reserved and have the following meanings:
-
<: open an object block; -
>: close an object block; -
=: indicate attribute value = object block; -
(,): type name or plug-in syntax type delimiters; -
<#: open an object block expressed in a plug-in syntax; -
#>: close an object block expressed in a plug-in syntax.
Within <> delimiters, various characters are used as follows to indicate primitive values:
-
": double quote characters are used to delimit string values; -
': single quote characters are used to delimit single character values; -
|: bar characters are used to delimit intervals; -
[]: brackets are used to delimit coded terms.
4.2.4. Comments
In a dADL text, comments satisfy the following rule.
Comments are indicated by the characters "--". Multi-line comments are achieved using the "--" leader on each line where the comment continues.
In this document, dADL comments are shown in brown.
4.2.5. Information Model Identifiers
Two types of identifiers from information models are used in dADL: type names and attribute names.
A type name is any identifier with an initial upper case letter, followed by any combination of letters, digits and underscores. A generic type name (including nested forms) additionally may include commas and angle brackets, and must be syntactically correct as per the UML. An attribute name is any identifier with an initial lower case letter, followed by any combination of letters, digits and underscores. Any convention that obeys this rule is allowed.
At least two well-known conventions that are ubiquitous in information models obey the above rule. One of these is the following convention:
-
type names are in all uppercase, e.g.
PERSON, except for 'built-in' types, such as primitive types (` Integer` ,String,Boolean,Real,Double) and assumed container types (List<T>,Set<T>,Hash<T, U>), which are in mixed case, in order to provide easy differentiation of built-in types from constructed types defined in the reference model. Built-in types are the same types assumed by UML, OCL, IDL and other similar object-oriented formalisms. -
attribute names are shown in all lowercase, e.g.
home_address. -
in both type names and attribute names, underscores are used to represent word breaks. This convention is used to maximise the readability of this document.
The other common style is the programmer’s mixed-case or "camel case" convention exemplified by Person and homeAddress , as long as they obey the rule above. The convention chosen for any particular dADL document should be based on the convention used in the underlying information model. Identifiers are shown in green in this document.
4.2.6. Semi-colons
Semi-colons can be used to separate dADL blocks, for example when it is preferable to include multiple attribute/value pairs on one line. Semi-colons make no semantic difference at all, and are included only as a matter of taste. The following examples are equivalent:
term = <text = <"plan">; description = <"The clinician's advice">>
term = <text = <"plan"> description = <"The clinician's advice">>
term = <
text = <"plan">
description = <"The clinician's advice">
>Semi-colons are completely optional in dADL.
4.3. Paths
Because dADL data is hierarchical, and all nodes are uniquely identified, a reliable path can be determined for every node in a dADL text. The syntax of paths in dADL is the standard ADL path syntax, described in detail in Section 7. Paths are directly convertible to XPath expressions for use in XML-encoded data.
A typical ADL path used to refer to a node in a dADL text is as follows.
/term_definitions["en"]/items["at0001"]/textIn the following sections, paths are shown for all the dADL data examples.
4.4. Structure
4.4.1. General Form
A dADL document expresses serialised instances of one or more complex objects. Each such instance is a hierarchy of attribute names and object values. In its simplest form, a dADL text consists of repetitions of the following pattern:
attribute_name '=' '<' value '>' ;
Each attribute name is the name of an attribute in an implied or actual object or relational model. Each "value" is either a literal value of a primitive type (see Section 4.5.1) or a further nesting of attribute names and values, terminating in leaf nodes of primitive type values. Where sibling attribute nodes occur, the attribute identifiers must be unique, just as in a standard object or relational model.
Sibling attribute names must be unique.
The following shows a typical structure.
attr_1 = <
attr_2 = <
attr_3 = <leaf_value>
attr_4 = <leaf_value>
>
attr_5 = <
attr_3 = <
attr_6 = <leaf_value>
>
attr_7 = <leaf_value>
>
>
attr_8 = <...>In the above structure, each "<>" encloses an instance of some type. The hierarchical structure corresponds to the part-of relationship between objects, otherwise known as composition and aggregation relationships in object-oriented formalisms such as UML (the difference between the two is usually described as being "sub-objects related by aggregation can have independent lifetimes, whereas sub-objects related by composition have co-termimal lifetimes and are always destroyed with the parent"; dADL does not differentiate between the two, since it is the business of a model, not the data, to express such semantics). Associations between instances in dADL are also representable by references, and are described in Section 4.4.6.
4.4.1.1. Outer Delimiters
To be completely regular, an outer level of delimiters should be used, because the totality of a dADL text is an object, not a collection of disembodied attribute/object pairs. However, the outermost delimiters can be left out in order to improve readability, and without complicating the parsing process. The completely regular form would appear as follows:
<
attr_1 = <
>
attr_8 = <>
>
Outer '<>' delimiters in a dADL text are optional.
4.4.1.2. Paths
The complete set of paths for the above example is as follows.
/attr_1
/attr_1/attr_2
/attr_1/attr_2/attr_3 -- path to a leaf value
/attr_1/attr_2/attr_4 -- path to a leaf value
/attr_1/attr_5
/attr_1/attr_5/attr_3
/attr_1/attr_5/attr_3/attr_6 -- path to a leaf value
/attr_1/attr_5/attr_7 -- path to a leaf value
/attr_8The path syntax used with dADL maps trivially to W3C Xpath and Xquery paths, and is described in Section 4.3.
4.4.2. Empty Sections
Empty sections are allowed at both internal and leaf node levels, enabling the author to express the fact that there is in some particular instance, no data for an attribute, while still showing that the attribute itself is expected to exist in the underlying information model. An empty section looks as follows:
address = <...> -- person's addressNested empty sections can be used.
|
Note
|
within this document, empty sections are shown in many places to represent fully populated data, which would of course require much more space. |
Empty sections can appear anywhere.
4.4.3. Container Objects
The syntax described so far allows an instance of an arbitrarily large object to be expressed, but does not support attributes of container types such as lists, sets and hash tables, i.e. items whose type in an underlying reference model is something like attr:List<Type> , attr:Set<Type> or attr: Hash<ValueType, KeyType> . There are two ways instance data of such container objects can be expressed in dADL. The first applies to leaf values and is to use a list style literal value for , where the "list nature" of the data is expressed within the manifest value itself, as in the following examples.
fruits = <"pear", "cumquat", "peach">
some_primes = <1, 2, 3, 5>See Section 4.5.4 for the complete description of list leaf types. This approach is fine for leaf data. However for containers holding non-primitive values, including more container objects, a different syntax is needed. Consider by way of example that an instance of the container List<Person> could in theory be expressed as follows.
-- WARNING: THIS IS NOT VALID dADL
people = <
<name = <...> date_of_birth = <...> sex = <...> interests = <...> >
<name = <...> date_of_birth = <...> sex = <...> interests = <...> >
-- etc
>Here, 'anonymous' blocks of data are repeated inside the outer block. However, this makes the data hard to read, and does not provide an easy way of constructing paths to the contained items. A better syntax becomes more obvious when we consider that members of container objects in their computable form are nearly always accessed by a method such as member(i) , item[i] or just plain [i] , in the case of array access in the C-based languages.
dADL opts for the array-style syntax, known in dADL as container member keys. No attribute name is explicitly given; any primitive comparable value is allowed as the key, rather than just integers used in C-style array access. Further, if integers are used, it is not assumed that they dictate ordinal indexing, i.e. it is possible to use a series of keys [2] , [4] , [8] etc. The following example shows one version of the above container in valid dADL:
people = <
[1] = <name = <...> birth_date = <...> interests = <...> >
[2] = <name = <...> birth_date = <...> interests = <...> >
[3] = <name = <...> birth_date = <...> interests = <...> >
>Strings and dates may also be used. Keys are coloured blue in the this specification in order to distinguish the run-time status of key values from the design-time status of class and attribute names. The following example shows the use of string values as keys for the contained items.
people = <
["akmal:1975-04-22"] = <name = <...> birth_date = <...> interests = <...> >
["akmal:1962-02-11"] = <name = <...> birth_date = <...> interests = <...> >
["gianni:1978-11-30"] = <name = <...> birth_date = <...> interests = <...> >
>The syntax for primitive values used as keys follows exactly the same syntax described below for data of primitive types. It is convenient in some cases to construct key values from one or more of the values of the contained items, in the same way as relational database keys are constructed from sufficient field values to guarantee uniqueness. However, they need not be - they may be independent of the contained data, as in the case of hash tables, where the keys are part of the hash table structure, or equally, they may simply be integer index values, as in the 'locations' attribute in the 'school_schedule' structure shown below.
Container structures can appear anywhere in an overall instance structure, allowing complex data such as the following to be expressed in a readable way.
school_schedule = <
lesson_times = <08:30:00, 09:30:00, 10:30:00, ...>
locations = <
[1] = <"under the big plane tree">
[2] = <"under the north arch">
[3] = <"in a garden">
>
subjects = <
["philosophy:plato"] = < -- note construction of key
name = <"philosophy">
teacher = <"plato">
topics = <"meta-physics", "natural science">
weighting = <76%>
>
["philosophy:kant"] = <
name = <"philosophy">
teacher = <"kant">
topics = <"meaning and reason", "meta-physics", "ethics">
weighting = <80%>
>
["art"] = <
name = <"art">
teacher = <"goya">
topics = <"technique", "portraiture", "satire">
weighting = <78%>
>
>
>Container instances are expressed using repetitions of a block introduced by a key, in the form of a primitive value in brackets i.e. '[]'.
The example above conforms directly to the object-oriented type specification (given in a pascal-like syntax):
class SCHEDULE
lesson_times: List<Time>
locations: List<String>
subjects: List<SUBJECT> -- or it could be Hash<SUBJECT>
end
class SUBJECT
name: String
teacher: String
topics: List<String>
weighting: Real
endOther class specifications corresponding to the same data are possible, but will all be isomorphic to the above.
How key values relate to a particular object structure depends on the object model being used during the dADL parsing process. It is possible to write a parser which makes reasonable inferences from an information model whose instances are represented as dADL text; it is also possible to include explicit typing information in the dADL itself (see Section 4.4.5 below).
4.4.3.1. Paths
Paths through container objects are formed in the same way as paths in other structured data, with the addition of the key, to ensure uniqueness. The key is included syntactically enclosed in brackets, in a similar way to Xpath predicates. Paths through containers in the above example include the following:
/school_schedule/locations[1] -- path to "under the big..."
/school_schedule/subjects["philosophy:kant"] -- path to "kant"4.4.4. Nested Container Objects
In some cases the data of interest are instances of nested container types, such as List<List<Message>> (a list of Message lists) or Hash<List<Integer>, String> (a hash of integer lists keyed by strings). The dADL syntax for such structures follows directly from the syntax for a single container object. The following example shows an instance of the type List<List<String>> expressed in dADL syntax.
list_of_string_lists = <
[1] = <
[1] = <"first string in first list">
[2] = <"second string in first list">
>
[2] = <
[1] = <"first string in second list">
[2] = <"second string in second list">
[3] = <"third string in second list">
>
[3] = <
[1] = <"only string in third list">
>
>4.4.5. Adding Type Information
In many cases, dADL data is of a simple structure, very regular, and highly repetitive, such as the expression of simple demographic data. In such cases, it is preferable to express as little as possible about the implied reference model of the data (i.e. the object or relational model to which it conforms), since various software components want to use the data, and use it in different ways. However, there are also cases where the data is highly complex, and more model information is needed to help software parse it,. Examples include large design databases such as for aircraft, and health records. Typing information is added to instance data using a syntactical addition inspired by the (type) casting operator of the C language, whose meaning is approximately: force the type of the result of the following expression to be type. In dADL typing is therefore done by including the type name in parentheses after the '=' sign, as in the following example.
destinations = <
["seville"] = (TOURIST_DESTINATION) <
profile = (DESTINATION_PROFILE) <...>
hotels = <
["gran sevilla"] = (HISTORIC_HOTEL) <...>
["sofitel"] = (LUXURY_HOTEL) <...>
["hotel real"] = (PENSION) <...>
>
attractions = <
["la corrida"] = (SPORT_VENUE) <...>
["Alcázar"] = (HISTORIC_SITE) <...>
>
>
>Note that in the above, no type identifiers are included after the "hotels" and "attractions" attributes, and it is up to the processing software to infer the correct types (usually easy - it will be pre-determined by an information model). However, the complete typing information can be included, as follows.
hotels = (List<HOTEL>) <
["gran sevilla"] = (HISTORIC_HOTEL) <>
>This illustrates the use of generic, i.e. template types, expressed in the standard UML syntax, using angle brackets. Any number of template arguments and any level of nesting is allowed, as in the UML. At first view, there may appear to be a risk of confusion between template type '<>' delimiters and the standard dADL block delimiters. However the parsing rules are easy to state; essentially the difference is that a dADL data block is always preceded by an '=' symbol.
Type identifiers can also include namespace information, which is necessary when same-named types appear in different packages of a model. Namespaces are included by prepending package names, separated by the '.' character, in the same way as in most programming languages, as in the qualified type names org.openehr.rm.ehr.content.ENTRY and Core.Abstractions.Relationships.Relationship.
Type Information can be included optionally on any node immediately before the opening '<' of any block, in the form of a UML-style type identifier in parentheses. Dot-separated namespace identifiers and template parameters may be used.
4.4.6. Associations and Shared Objects
All of the facilities described so far allow any object-oriented data to be faithfully expressed in a formal, systematic way which is both machine- and human-readable, and allow any node in the data to be addressed using an Xpath-style path. The availability of reliable paths allows not only the representation of single 'business objects', which are the equivalent of UML aggregation (and composition) hierarchies, but also the representation of associations between objects, and by extension, shared objects.
Consider that in the example above, 'hotel' objects may be shared objects, referred to by association. This can be expressed as follows.
destinations = <
["seville"] = <
hotels = <
["gran sevilla"] = </hotels["gran sevilla"]>
["sofitel"] = </hotels["sofitel"]>
["hotel real"] = </hotels["hotel real"]>
>
>
>
bookings = <
["seville:0134"] = <
customer_id = <"0134">
period = <...>
hotel = </hotels["sofitel"]>
>
>
hotels = <
["gran sevilla"] = (HISTORIC_HOTEL) <>
["sofitel"] = (LUXURY_HOTEL) <>
["hotel real"] = (PENSION) <>
>Associations are expressed via the use of fully qualified paths as the data for an attribute. In this example, there are references from a list of destinations, and from a booking list, to the same hotel object. If type information is included, it should go in the declarations of the relevant objects; type declarations can also be used before path references, which might be useful if the association type is an ancestor type (i.e. more general type) of the type of the actual object being referred to.
Data in other dADL documents can be referred to using the URI syntax to locate the document, with the internal path included as described above.
Shared objects are referenced using paths. Objects in other dADL documents can be referred to using normal URIs whose path section conforms to dADL path syntax.
4.4.6.1. Paths
The path set from the above example is as follows:
/destinations["seville"]/hotels["gran sevilla"]
/destinations["seville"]/hotels["sofitel"]
/destinations["seville"]/hotels["hotel real"]
/bookings["seville:0134"]/customer_id
/bookings["seville:0134"]/period
/bookings["seville:0134"]/hotel
/hotels["sofitel"]
/hotels["hotel real"]
/hotels["gran sevilla"]4.5. Leaf Data - Built-in Types
All dADL data eventually devolve to instances of the primitive types String, Integer, Real, Double, String, Character, various date/time types, lists or intervals of these types, and a few special types. dADL does not use type or attribute names for instances of primitive types, only manifest values, making it possible to assume as little as possible about type names and structures of the primitive types. In all the following examples, the manifest data values are assumed to appear immediately inside a leaf pair of angle brackets, i.e.
some_attribute = <manifest value here>
4.5.1. Primitive Types
4.5.1.1. Character Data
Characters are shown in a number of ways. In the literal form, a character is shown in single quotes, as follows:
'a'
Characters outside the low ASCII (0-127) range must be UTF-8 encoded, with a small number of backslash-quoted ASCII characters allowed, as described in Section 3.
4.5.1.2. String Data
All strings are enclosed in double quotes, as follows:
"this is a string"
Quotes are encoded using ISO/IEC 10646 codes, e.g. :
"this is a much longer string, what one might call a "phrase"."
Line extension of strings is done simply by including returns in the string. The exact contents of the string are computed as being the characters between the double quote characters, with the removal of white space leaders up to the left-most character of the first line of the string. This has the effect of allowing the inclusion of multi-line strings in dADL texts, in their most natural human-readable form, e.g.:
text = <"And now the STORM-BLAST came, and he
Was tyrannous and strong :
He struck with his o'ertaking wings,
And chased us south along.">String data can be used to contain almost any other kind of data, which is intended to be parsed as some other formalism. Characters outside the low ASCII (0-127) range must be UTF-8 encoded, with a small number of backslash-quoted ASCII characters allowed, as described in Section 3.
4.5.1.3. Integer Data
Integers are represented simply as numbers, e.g.:
25 300000 29e6
Commas or periods for breaking long numbers are not allowed, since they confuse the use of commas used to denote list items (see Section 4.5.4 below).
4.5.1.4. Real Data
Real numbers are assumed whenever a decimal is detected in a number, e.g.:
25.0 3.1415926 6.023e23
Commas or periods for breaking long numbers are not allowed. Only periods may be used to separate the decimal part of a number; unfortunately, the European use of the comma for this purpose conflicts with the use of the comma to distinguish list items (see Section 4.5.4 below).
4.5.1.5. Boolean Data
Boolean values can be indicated by the following values (case-insensitive):
True False
4.5.1.6. Dates and Times
Complete Date/Times
In dADL, full and partial dates, times and durations can be expressed. All full dates, times and durations are expressed using a subset of ISO8601. The Support IM provides a full explanation of the ISO8601 semantics supported in openEHR.
In dADL, the use of ISO 8601 allows extended form only (i.e. ':' and '-' must be used). The ISO 8601 method of representing partial dates consisting of a single year number, and partial times consisting of hours only are not supported, since they are ambiguous. See below for partial forms. Patterns for complete dates and times in dADL include the following:
yyyy-MM-dd -- a date hh:mm:ss[,sss][Z|+/-hhmm] -- a time with optional seconds yyyy-MM-ddThh:mm:ss[,sss][Z] -- a date/time
where:
yyyy = four-digit year MM = month in year dd = day in month hh = hour in 24 hour clock mm = minutes ss,sss = seconds, incuding fractional part Z = the timezone in the form of a '+' or '-' followed by 4 digits indicating the hour offset, e.g. +0930, or else the literal 'Z' indicating +0000 (the Greenwich meridian).
Durations are expressed using a string which starts with 'P', and is followed by a list of periods, each appended by a single letter designator: 'Y' for years, "M' for months, 'W' for weeks, 'D' for days, 'H' for hours, 'M' for minutes, and 'S' for seconds. The literal 'T' separates the YMWD part from the HMS part, ensuring that months and minutes can be distinguished. Examples of date/time data include:
1919-01-23 -- birthdate of Django Reinhardt 16:35:04,5 -- rise of Venus in Sydney on 24 Jul 2003 2001-05-12T07:35:20+1000 -- timestamp on an email received from Australia P22D4TH15M0S -- period of 22 days, 4 hours, 15 minutes
Partial Date/Times
Two ways of expressing partial (i.e. incomplete) date/times are supported in dADL. The ISO 8601 incomplete formats are supported in extended form only (i.e. with '-' and ':' separators) for all patterns that are unambiguous on their own. Dates consisting of only the year, and times consisting of only the hour are not supported, since both of these syntactically look like integers. The supported ISO 8601 patterns are as follows:
yyyy-MM -- a date with no days hh:mm -- a time with no seconds yyyy-MM-ddThh:mm -- a date/time with no seconds yyyy-MM-ddThh -- a date/time, no minutes or seconds
To deal with the limitations of ISO 8601 partial patterns in a context-free parsing environment, a second form of pattern is supported in dADL, based on ISO 8601. In this form, '?' characters are substituted for missing digits. Valid partial dates follow the patterns:
yyyy-MM-?? -- date with unknown day in month yyyy-??-?? -- date with unknown month and day
Valid partial times follow the patterns:
hh:mm:?? -- time with unknown seconds hh:??:?? -- time with unknown minutes and seconds
Valid date/times follow the patterns:
yyyy-MM-ddThh:mm:?? -- date/time with unknown seconds yyyy-MM-ddThh:??:?? -- date/time with unknown minutes and seconds yyyy-MM-ddT??:??:?? -- date/time with unknown time yyyy-MM-??T??:??:?? -- date/time with unknown day and time yyyy-??-??T??:??:?? -- date/time with unknown month, day and time
4.5.2. Intervals of Ordered Primitive Types
Intervals of any ordered primitive type, i.e., Integer, Real, Date, Time, Date_time and Duration, can be stated using the following uniform syntax, where N, M are instances of any of the ordered types:
|N..M| -- the two-sided range N >= x <= M |N>..M| -- the two-sided range N > x <= M |N..<M| -- the two-sided range N >= x <M |N>..<M| -- the two-sided range N > x <M |<N| -- the one-sided range x < N |>N| -- the one-sided range x > N |>=N| -- the one-sided range x >= N |<=N| -- the one-sided range x <= N |N +/-M| -- interval of N ± M
The allowable values for N and M include any value in the range of the relevant type, as well as:
infinity -infinity * equivalent to infinity
Examples of this syntax include:
|0..5| -- integer interval |0.0..1000.0| -- real interval |0.0..<1000.0| -- real interval 0.0 >= x < 1000.0 |08:02..09:10| -- interval of time |>= 1939-02-01| -- open-ended interval of dates |5.0 +/-0.5| -- 4.5 - 5.5 |>=0| -- >= 0 |0..infinity| -- 0 - infinity (i.e. >= 0)
4.5.3. Other Built-in Types
4.5.3.1. URIs
URI can be expressed as dADL data in the usual way found on the web, and follow the standard syntax from http://www.ietf.org/rfc/rfc3986.txt. Examples of URIs in dADL:
http://archetypes.are.us/home.html ftp://get.this.file.com#section_5 http://www.mozilla.org/products/firefox/upgrade/?application=thunderbird
Encoding of special characters in URIs follows the IETF RFC 3986, as described under Section 3.
4.5.3.2. Coded Terms
Coded terms are ubiquitous in medical and clinical information, and are likely to become so in most other industries, as ontologically-based information systems and the 'semantic web' emerge. The logical structure of a coded term is simple: it consists of an identifier of a terminology, and an identifier of a code within that terminology. The dADL string representation is as follows:
[terminology_id::code]
Typical examples from clinical data:
[icd10AM::F60.1] -- from ICD10AM [snomed-ct::2004950] -- from snomed-ct [snomed-ct(3.1)::2004950] -- from snomed-ct v 3.1
4.5.4. Lists of Built-in Types
Data of any primitive type can occur singly or in lists, which are shown as comma-separated lists of item, all of the same type, such as in the following examples:
"cyan", "magenta", "yellow", "black" -- printer's colours 1, 1, 2, 3, 5 -- first 5 fibonacci numbers 08:02, 08:35, 09:10 -- set of train times
No assumption is made in the syntax about whether a list represents a set, a list or some other kind of sequence - such semantics must be taken from an underlying information model.
Lists which happen to have only one datum are indicated by using a comma followed by a list continuation marker of three dots, i.e. "…", e.g.:
"en", ... -- languages "icd10", ... -- terminologies [at0200], ...
White space may be freely used or avoided in lists, i.e. the following two lists are identical:
1,1,2,3 1, 1, 2,3
4.6. Plug-in Syntaxes
Using the dADL syntax, any object structure can be serialised. In some cases, the requirement is to express some part of the structure in an abstract syntax, rather than in the more literal seriliased object form of dADL. dADL provides for this possibility by allowing the value of any object (i.e. what appears between any matching pair of <> delimiters) to be expressed in some other syntax, known as a "plug-in" syntax. Plug-in syntaxes are indicated in dADL in a similar way as typed objects, i.e. by the use of the syntax type in parentheses preceding the <> block. For a plug-in section, the <> delimiters are modified to <# #>, to allow for easier parser design, and easier recognition of such blocks by human readers. The general form is as follows:
attr_name = (syntax) <#
...
#>
The following example illustrates a cADL plug-in section in an archetype, which it itself a dADL document:
definition = (cadl) <#
ENTRY[at0000] ∈ { -- blood pressure measurement
name ∈ { -- any synonym of BP
CODED_TEXT ∈ {
code ∈ {
CODE_PHRASE ∈ {[ac0001]}
}
}
}
}
#>
Clearly, many plug-in syntaxes might one day be used within dADL data; there is no guarantee that every dADL parser will support them. The general approach to parsing should be to use plug-in parsers, i.e. to obtain a parser for a plug-in syntax that can be built into the existing parser framework.
4.7. Expression of dADL in XML
The dADL syntax maps quite easily to XML instance. It is important to realise that people using XML often develop different mappings for object-oriented data, due to the fact that XML does not have systematic object-oriented semantics. This is particularly the case where containers such as lists and sets such as employees: List<Person> are mapped to XML; many implementors have to invent additional tags such as 'employee' to make the mapping appear visually correct. The particular mapping chosen here is designed to be a faithful reflection of the semantics of the object-oriented data, and does not try take into account visual aesthetics of the XML. The result is that Xpath expressions are the same for dADL and XML, and also correspond to what one would expect based on an underlying object model. The main elements of the mapping are as follows.
4.7.2. Container Attributes
Container attribute nodes map to a series of tagged nodes of the same name, each with the XML attribute id set to the dADL key. For example, the dADL:
subjects = <
["philosophy:plato"] = <
name = <"philosophy">
>
["philosophy:kant"] = <
name = <"philosophy">
>
>maps to the XML:
<subjects id="philosophy:plato">
<name>
philosophy
</name>
</subjects>
<subjects id="philosophy:kant">
<name>
philosophy
</name>
</subjects>This guarantees that the path subjects[@id="philosophy:plato"]/name navigates to the same element in both dADL and the XML.
4.7.3. Nested Container Attributes
Nested container attribute nodes map to a series of tagged nodes of the same name, each with the XML attribute id set to the dADL key. For example, consider an object structure defined by the signature countries:Hash<Hash<Hotel,String>,String>. An instance of this in dADL looks as follows:
countries = <
["spain"] = <
["hotels"] = <...>
["attractions"] = <...>
>
["egypt"] = <
["hotels"] = <...>
["attractions"] = <...>
>
>can be mapped to the XML in which the synthesised element tag "_items" and the attribute "key" are used:
<countries key="spain">
<_items key="hotels">
...
</_items>
<_items key="attractions">
...
</_items>
</countries>
<countries key="eqypt">
<_items id="hotels">
...
</_items>
<_items key="attractions">
...
</_items>
</countries>In this case, the dADL path countries["spain"]/["hotels"] will be transformed to the Xpath countries[@key="spain"]/_items[@key="hotels"] in order to navigate to the same element.
4.7.4. Type Names
Type names map to XML 'type' attributes e.g. the dADL:
destinations = <
["seville"] = (TOURIST_DESTINATION) <
profile = (DESTINATION_PROFILE) <>
hotels = <
["gran sevilla"] = (HISTORIC_HOTEL) <>
>
>
>maps to:
<destinations id="seville" adl:type="TOURIST_DESTINATION">
<profile adl:type="DESTINATION_PROFILE">
...
</profile>
<hotels id="gran sevilla" adl:type="HISTORIC_HOTEL">
...
</hotels>
</destinations>4.8. Syntax Specification
The grammar and lexical specification for the standard dADL syntax is shown below. This grammar is implemented using lex (.l file) and yacc (.y file) specifications for in the Eiffel programming environment. The current release of these files is available at Tag Release-1.4 of the adl-tools Github repository. The .l and .y files can be converted for use in another yacc/lexbased programming environment. The dADL production rules are also available as an HTML document.
4.8.1. Grammar
The following provides the dADL parser production rules (yacc specification).
input:
attr_vals
| complex_object_block
;
attr_vals:
attr_val
| attr_vals attr_val
| attr_vals ';' attr_val
;
attr_val:
attr_id SYM_EQ object_block
;
attr_id:
V_ATTRIBUTE_IDENTIFIER
;
object_block:
complex_object_block
| primitive_object_block
| plugin_object_block
;
plugin_object_block:
V_PLUGIN_SYNTAX_TYPE V_PLUGIN_BLOCK
;
complex_object_block:
single_attr_object_block
| multiple_attr_object_block
;
multiple_attr_object_block:
untyped_multiple_attr_object_block
| type_identifier untyped_multiple_attr_object_block
;
untyped_multiple_attr_object_block:
multiple_attr_object_block_head keyed_objects SYM_END_DBLOCK
;
multiple_attr_object_block_head:
SYM_START_DBLOCK
;
keyed_objects:
keyed_object
| keyed_objects keyed_object
;
keyed_object:
object_key SYM_EQ object_block
;
object_key:
'[' simple_value ']'
;
single_attr_object_block:
untyped_single_attr_object_block
| type_identifier untyped_single_attr_object_block
;
untyped_single_attr_object_block:
single_attr_object_complex_head SYM_END_DBLOCK
| single_attr_object_complex_head attr_vals SYM_END_DBLOCK
;
single_attr_object_complex_head:
SYM_START_DBLOCK
primitive_object_block:
untyped_primitive_object_block
| type_identifier untyped_primitive_object_block
;
untyped_primitive_object_block:
SYM_START_DBLOCK primitive_object_value SYM_END_DBLOCK
;
primitive_object_value:
simple_value
| simple_list_value
| simple_interval_value
| term_code
| term_code_list_value
;
simple_value:
string_value
| integer_value
| real_value
| boolean_value
| character_value
| date_value
| time_value
| date_time_value
| duration_value
| uri_value
;
simple_list_value:
string_list_value
| integer_list_value
| real_list_value
| boolean_list_value
| character_list_value
| date_list_value
| time_list_value
| date_time_list_value
| duration_list_value
;
simple_interval_value:
integer_interval_value
| real_interval_value
| date_interval_value
| time_interval_value
| date_time_interval_value
| duration_interval_value
;
type_identifier:
'(' V_TYPE_IDENTIFIER ')'
| '(' V_GENERIC_TYPE_IDENTIFIER ')'
| V_TYPE_IDENTIFIER
| V_GENERIC_TYPE_IDENTIFIER
;
string_value:
V_STRING
;
string_list_value:
V_STRING ',' V_STRING
| string_list_value ',' V_STRING
| V_STRING ',' SYM_LIST_CONTINUE
;
integer_value:
V_INTEGER
| '+' V_INTEGER
| '-' V_INTEGER
;
integer_list_value:
integer_value ',' integer_value
| integer_list_value ',' integer_value
| integer_value ',' SYM_LIST_CONTINUE
;
integer_interval_value:
SYM_INTERVAL_DELIM integer_value SYM_ELLIPSIS integer_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM SYM_GT integer_value SYM_ELLIPSIS integer_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM integer_value SYM_ELLIPSIS SYM_LT integer_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM SYM_GT integer_value SYM_ELLIPSIS SYM_LT integer_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM SYM_LT integer_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM SYM_LE integer_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM SYM_GT integer_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM SYM_GE integer_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM integer_value SYM_INTERVAL_DELIM
;
real_value:
V_REAL
| '+' V_REAL
| '-' V_REAL
;
real_list_value:
real_value ',' real_value
| real_list_value ',' real_value
| real_value ',' SYM_LIST_CONTINUE
;
real_interval_value:
SYM_INTERVAL_DELIM real_value SYM_ELLIPSIS real_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM SYM_GT real_value SYM_ELLIPSIS real_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM real_value SYM_ELLIPSIS SYM_LT real_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM SYM_GT real_value SYM_ELLIPSIS SYM_LT real_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM SYM_LT real_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM SYM_LE real_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM SYM_GT real_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM SYM_GE real_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM real_value SYM_INTERVAL_DELIM
;
boolean_value:
SYM_TRUE
| SYM_FALSE
;
boolean_list_value:
boolean_value ',' boolean_value
| boolean_list_value ',' boolean_value
| boolean_value ',' SYM_LIST_CONTINUE
;
character_value:
V_CHARACTER
;
character_list_value:
character_value ',' character_value
| character_list_value ',' character_value
| character_value ',' SYM_LIST_CONTINUE
;
date_value:
V_ISO8601_EXTENDED_DATE
;
date_list_value:
date_value ',' date_value
| date_list_value ',' date_value
| date_value ',' SYM_LIST_CONTINUE
;
date_interval_value:
SYM_INTERVAL_DELIM date_value SYM_ELLIPSIS date_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM SYM_GT date_value SYM_ELLIPSIS date_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM date_value SYM_ELLIPSIS SYM_LT date_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM SYM_GT date_value SYM_ELLIPSIS SYM_LT date_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM SYM_LT date_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM SYM_LE date_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM SYM_GT date_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM SYM_GE date_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM date_value SYM_INTERVAL_DELIM
;
time_value:
V_ISO8601_EXTENDED_TIME
time_list_value:
time_value ',' time_value
| time_list_value ',' time_value
| time_value ',' SYM_LIST_CONTINUE
;
time_interval_value:
SYM_INTERVAL_DELIM time_value SYM_ELLIPSIS time_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM SYM_GT time_value SYM_ELLIPSIS time_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM time_value SYM_ELLIPSIS SYM_LT time_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM SYM_GT time_value SYM_ELLIPSIS SYM_LT time_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM SYM_LT time_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM SYM_LE time_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM SYM_GT time_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM SYM_GE time_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM time_value SYM_INTERVAL_DELIM
;
date_time_value:
V_ISO8601_EXTENDED_DATE_TIME
;
date_time_list_value:
date_time_value ',' date_time_value
| date_time_list_value ',' date_time_value
| date_time_value ',' SYM_LIST_CONTINUE
;
date_time_interval_value:
SYM_INTERVAL_DELIM date_time_value SYM_ELLIPSIS date_time_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM SYM_GT date_time_value SYM_ELLIPSIS date_time_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM date_time_value SYM_ELLIPSIS SYM_LT date_time_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM SYM_GT date_time_value SYM_ELLIPSIS SYM_LT date_time_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM SYM_LT date_time_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM SYM_LE date_time_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM SYM_GT date_time_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM SYM_GE date_time_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM date_time_value SYM_INTERVAL_DELIM
;
duration_value:
V_ISO8601_DURATION
;
duration_list_value:
duration_value ',' duration_value
| duration_list_value ',' duration_value
| duration_value ',' SYM_LIST_CONTINUE
;
duration_interval_value:
SYM_INTERVAL_DELIM duration_value SYM_ELLIPSIS duration_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM SYM_GT duration_value SYM_ELLIPSIS duration_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM duration_value SYM_ELLIPSIS SYM_LT duration_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM SYM_GT duration_value SYM_ELLIPSIS SYM_LT duration_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM SYM_LT duration_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM SYM_LE duration_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM SYM_GT duration_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM SYM_GE duration_value SYM_INTERVAL_DELIM
| SYM_INTERVAL_DELIM duration_value SYM_INTERVAL_DELIM
;
term_code:
V_QUALIFIED_TERM_CODE_REF
term_code_list_value:
term_code ',' term_code
| term_code_list_value ',' term_code
| term_code ',' SYM_LIST_CONTINUE
;
uri_value:
V_URI
;4.8.2. Symbols
The following provides the dADL lexical analyser production rules (lex specification) used in the Release-1.4 parser:
----------/* definitions */ -----------------------------------------------
ALPHANUM [a-zA-Z0-9]
IDCHAR [a-zA-Z0-9_]
NAMECHAR [a-zA-Z0-9._\-]
NAMECHAR_SPACE [a-zA-Z0-9._\- ]
NAMECHAR_PAREN [a-zA-Z0-9._\-()]
UTF8CHAR (([\xC2-\xDF][\x80-\xBF])|(\xE0[\xA0-\xBF][\x80-\xBF])|([\xE1-\xEF][\x80-\xBF][\x80-\xBF])|(\xF0[\x90-\xBF][\x80-\xBF][\x80-\xBF])|([\xF1-\xF7][\x80-\xBF][\x80-\xBF][\x80-\xBF]))
----------/** Separators **/---------------------------------------------
[ \t\r]+ -- Ignore separators
\n+ -- (increment line count)
----------/** comments **/-----------------------------------------------
"--".* -- Ignore comments
"--".*\n[ \t\r]* -- (increment line count)
----------/* symbols */ -------------------------------------------------
"-" -- -> Minus_code
"+" -- -> Plus_code
"*" -- -> Star_code
"/" -- -> Slash_code
"^" -- -> Caret_code
"." -- -> Dot_code
";" -- -> Semicolon_code
"," -- -> Comma_code
":" -- -> Colon_code
"!" -- -> Exclamation_code
"(" -- -> Left_parenthesis_code
")" -- -> Right_parenthesis_code
"$" -- -> Dollar_code
"??" -- -> SYM_DT_UNKNOWN
"?" -- -> Question_mark_code
"|" -- -> SYM_INTERVAL_DELIM
"[" -- -> Left_bracket_code
"]" -- -> Right_bracket_code
"=" -- -> SYM_EQ
">=" -- -> SYM_GE
"<=" -- -> SYM_LE
"<" -- -> SYM_LT or SYM_START_DBLOCK
">" -- -> SYM_GT or SYM_END_DBLOCK
".." -- -> SYM_ELLIPSIS
"..." -- -> SYM_LIST_CONTINUE
----------/* keywords */ ---------------------------------------------
[Tt][Rr][Uu][Ee] -- -> SYM_TRUE
[Ff][Aa][Ll][Ss][Ee] -- -> SYM_FALSE
[Ii][Nn][Ff][Ii][Nn][Ii][Tt][Yy] -- -> SYM_INFINITY
----------/* V_URI */ -------------------------------------------------
[a-z]+:\/\/[^<>|\\{}^~"\[\] ]*
----------/* V_QUALIFIED_TERM_CODE_REF form [ICD10AM(1998)::F23] */ -----
\[{NAMECHAR_PAREN}+::{NAMECHAR}+\]
----------/* ERR_V_QUALIFIED_TERM_CODE_REF */ -----
\[{NAMECHAR_PAREN}+::{NAMECHAR_SPACE}+\]
----------/* V_LOCAL_TERM_CODE_REF */ ---------------------------------
\[{ALPHANUM}{NAMECHAR}*\]
----------/* V_LOCAL_CODE */ ------------------------------------------
a[ct][0-9.]+
----------/* V_ISO8601_EXTENDED_DATE_TIME YYYY-MM-DDThh:mm:ss[,sss][Z|+/-nnnn] */ ---
[0-9]{4}-[0-1][0-9]-[0-3][0-9]T[0-2][0-9]:[0-6][0-9]:[0-6][0-9](,[0-9]+)?(Z|[+-][0-9]{4})? |
[0-9]{4}-[0-1][0-9]-[0-3][0-9]T[0-2][0-9]:[0-6][0-9](Z|[+-][0-9]{4})? |
[0-9]{4}-[0-1][0-9]-[0-3][0-9]T[0-2][0-9](Z|[+-][0-9]{4})?
----------/* V_ISO8601_EXTENDED_TIME hh:mm:ss[,sss][Z|+/-nnnn] */ --------
[0-2][0-9]:[0-6][0-9]:[0-6][0-9](,[0-9]+)?(Z|[+-][0-9]{4})? |
[0-2][0-9]:[0-6][0-9](Z|[+-][0-9]{4})?
----------/* V_ISO8601_EXTENDED_DATE YYYY-MM-DD */ ------------------------
[0-9]{4}-[0-1][0-9]-[0-3][0-9] |
[0-9]{4}-[0-1][0-9]
----------/* V_ISO8601_DURATION PnYnMnWnDTnnHnnMnnS */ -------------
-- here we allow a deviation from the standard to allow weeks to be
-- mixed in with the rest since this commonly occurs in medicine
P([0-9]+[yY])?([0-9]+[mM])?([0-9]+[wW])?([0-9]+[dD])?T([0-9]+[hH])?([0-9]+[mM])?([0-9]+[sS])? |
P([0-9]+[yY])?([0-9]+[mM])?([0-9]+[wW])?([0-9]+[dD])?
----------/* V_TYPE_IDENTIFIER */ ---------------------------------------
[A-Z]{IDCHAR}*
----------/* V_GENERIC_TYPE_IDENTIFIER */ -------------------------------
[A-Z]{IDCHAR}*<[a-zA-Z0-9,_<>]+>
----------/* V_ATTRIBUTE_IDENTIFIER */ ----------------------------------
[a-z]{IDCHAR}*
----------/* CADL Blocks */ -------------------------------------------
\{[^{}]* -- beginning of CADL block
<IN_CADL_BLOCK>\{[^{}]* -- got an open brace
<IN_CADL_BLOCK>[^{}]*\} -- got a close brace
----------/* V_INTEGER */ ----------------------------------------------
[0-9]+ |
[0-9]+[eE][+-]?[0-9]+
----------/* V_REAL */ -------------------------------------------------
[0-9]+\.[0-9]+|
[0-9]+\.[0-9]+[eE][+-]?[0-9]+
----------/* V_STRING */ -----------------------------------------------
\"[^\\\n"]*\"
\"[^\\\n"]*{ -- beginning of a multi-line string
<IN_STR> {
\\\\ -- match escaped backslash, i.e. \\ -> \
\\\" -- match escaped double quote, i.e. \" -> "
{UTF8CHAR}+ -- match UTF8 chars
[^\\\n"]+ -- match any other characters
\\\n[ \t\r]* -- match LF in line
[^\\\n"]*\" -- match final end of string
.|\n |
<<EOF>> -- unclosed String -> ERR_STRING
}
----------/* V_CHARACTER */ --------------------------------------------
\'[^\\\n']\' -- normal character in 0-127
\'\\n\ -- \n
\'\\r\ -- \r
\'\\t\ -- \t
\'\\'\ -- \'
\'\\\\ -- \\
\'{UTF8CHAR}\' -- UTF8 char
\'.{1,2} |
\'\\[0-9]+(\/)? -- invalid character -> ERR_CHARACTER
4.9. Syntax Alternatives
|
Warning
|
the syntax in this section is not part of dADL |
4.9.1. Container Attributes
A reasonable alternative to the syntax described above for nested container objects would have been to use an arbitrary member attribute name, such as "items", or perhaps "_items" (in order to indicate to a parser that the attribute name cannot be assumed to correspond to a real property in an object model), as well as the key for each container member, giving syntax like the following:
people = <
_items[1] = <name = <> birth_date = <> interests = <>>
_items[2] = <name = <> birth_date = <> interests = <>>
_items[3] = <name = <> birth_date = <> interests = <>>
>
Additionally, with this alternative, it becomes more obvious how to include the values of other properties of container types, such as ordering, maximum size and so on, e.g.:
people = <
_items[1] = <name = <> birth_date = <> interests = <>>
_items[2] = <name = <> birth_date = <> interests = <>>
_items[3] = <name = <> birth_date = <> interests = <>>
_is_ordered = <True>
_upper = (200)
>
Again, since the names of such properties in any given object technology cannot be assumed, the special underscore form of attribute names is used. However, we are now led to somewhat clumsy paths, where "_items" will occur very frequently, due to the ubiquity of containers in real data:
/people/_items[1]/ /people/_items[2]/ /people/_items[3]/ /people/_is_ordered/ /people/_upper/
A compromise which satisfies the need for correct representation of all attributes of container types and the need for brevity and comprehensibility of paths would be to make optional the "_items", but retain other container pseudo-attributes (likely to be much more rarely used), thus:
people = <
[1] = <name = <> birth_date = <> interests = <>>
[2] = <name = <> birth_date = <> interests = <>>
[3] = <name = <> birth_date = <> interests = <>>
_is_ordered = <True>
_upper = (200)
>
The above form leads to the following paths:
/people[1]/ /people[2]/ /people[3]/ /people/_is_ordered/ /people/_upper/
The alternative syntax in this sub-section is not currently part of dADL, but could be included in the future, if there was a need to support more precise modelling of container types in dADL. If such support were to be added, it is recommended that the names of the pseudo-attributes ("_item", "_is_ordered" etc) be based on names of appopriate container types from a recognised standard such as OMG UML, OCL or IDL.
5. cADL - Constraint ADL
5.1. Overview
cADL is a syntax which enables constraints on data defined by object-oriented information models tobe expressed in archetypes or other knowledge definition formalisms. It is most useful for defining the specific allowable constructions of data whose instances conform to very general object models. cADL is used both at "design time", by authors and/or tools, and at runtime, by computational systems which validate data by comparing it to the appropriate sections of cADL in an archetype. The general appearance of cADL is illustrated by the following example:
PERSON[at0000] matches { -- constraint on a PERSON instance
name matches { -- constraint on PERSON.name
TEXT matches {/.+/} -- any non-empty string
}
addresses cardinality matches {0..*} matches { -- constraint on
ADDRESS matches { -- PERSON.addresses
-- etc --
}
}
}Some of the textual keywords in this example can be more efficiently rendered using common mathematical logic symbols. In the following example, the matches keyword has been replaced by an equivalent symbol:
PERSON[at0000] ∈ { -- constraint on a PERSON instance
name ∈ { -- constraint on PERSON.name
TEXT ∈ {/..*/} -- any non-empty string
}
addresses cardinality ∈ {1..*} ∈ { -- constraint on
ADDRESS ∈ { -- PERSON.addresses
-- etc --
}
}
}The full set of equivalences appears below. Raw cADL is stored in the text-based form, to remove any difficulties with representation of symbols, to avoid difficulties of authoring cADL text in normal text editors which do not supply such symbols, and to aid reading in English. However, the symbolic form might be more widely used due to the use of tools, and formatting in HTML and other documentary formats, and may be more comfortable for non-English speakers and those with formal mathematical backgrounds. This document uses both conventions. The use of symbols or text is completely a matter of taste, and no meaning whatsoever is lost by completely ignoring one or other format according to one’s personal preference.
In the standard cADL documented in this section, literal leaf values (such as the regular expression /..*/ in the above example) are always constraints on a set of 'standard' widely-accepted primitive types, as described in Section 4.
5.2. Basics
5.2.1. Keywords
The following keywords are recognised in cADL:
-
matches,~matches,is_in,~is_in -
occurrences,existence,cardinality -
ordered,unordered,unique -
infinity -
use_node, allow_archetype -
include,exclude -
before,after
Symbol equivalents for some of the above are given in the following table.
| Textual Rendering |
Symbolic Rendering |
Meaning |
|---|---|---|
matches |
∈ |
Set membership, "p is in P" |
not, ~ |
∼ |
Negation, "not p" |
Keywords are shown in blue in this document.
The matches or is_in operator deserves special mention, since it is a key operator in cADL. This operator can be understood mathematically as set membership. When it occurs between a name and a block delimited by braces, the meaning is: the set of values allowed for the entity referred to by the name (either an object, or parts of an object - attributes) is specified between the braces. What appears between any matching pair of braces can be thought of as a specification for a set of values. Since blocks can be nested, this approach to specifying values can be understood in terms of nested sets, or in terms of a value space for objects of a set of defined types. Thus, in the following example, the matches operator links the name of an entity to a linear value space (i.e. a list), consisting of all words ending in "ion".
aaa matches {/.*ion[^\s\n\t]/} -- the set of english words ending in 'ion'The following example links the name of a type XXX with a complex multi-dimensional value space.
XXX matches {
aaa matches { --
YYY matches {0..3} --
} -- the value space of the
bbb matches { -- and instance of XXX
ZZZ matches {>1992-12-01} --
} --
}The meaning of the constraint structure above is: in data matching the constraints, there is an instance of type XXX whose attribute values recursively match the inner constraints named after those attributes, and so on, to the leaf level.
Occasionally, the matches operator needs to be used in the negative, usually at a leaf block. Any of the following can be used to constrain the value space of the attribute aaa to any number except 5:
aaa ~matches {5}
aaa ~is_in {5}
aaa ∉ {5}The choice of whether to use matches or is_in is a matter of taste and background; those with a mathematical background will probably prefer is_in, while those with a data processing background may prefer matches.
5.2.2. Comments
In a cADL text, comments satisfy the following rule:
Comments are indicated by the leader characters '--'. Multi-line comments are achieved using the '--' leader on each line where the comment continues.
In this document, comments are shown in brown.
5.2.2.1. Information Model Identifiers
As with dADL, identifiers from the underlying information model are used for all cADL nodes. Identifiers obey the same rules as in dADL: type names commence with an upper case letter, while attribute and function names commence with a lower case letter. In cADL, type names and any property (i.e. attribute or function) name can be used, whereas in dADL, only type names and attribute names appear.
A type name is any identifier with an initial upper case letter, followed by any combination of letters, digits and underscores. A generic type name (including nested forms) additionally may include commas, angle brackets and spaces, and must be syntactically correct as per the UML. An attribute name is any identifier with an initial lower case letter, followed by any combination of letters, digits and underscores. Any convention that obeys this rule is allowed.
Type identifiers are shown in this document in all uppercase, e.g. PERSON , while attribute identifiers are shown in all lowercase, e.g. home_address . In both cases, underscores are used to represent word breaks. This convention is used to improve the readability of this document, and other conventions may be used, such as the common programmer’s mixed-case convention exemplified by Person and homeAddress. The convention chosen for any particular cADL document should be based on that used in the underlying information model. Identifiers are shown in blue in this document.
5.2.3. Node Identifiers
In cADL, an entity in brackets e.g. [xxxx] is used to identify "object nodes", i.e. nodes expressing constraints on instances of some type. Object nodes always commence with a type name. Any string may appear within the brackets, depending on how it is used. However, in this document, all node identifiers are of the form of an archetype term identifier, i.e. [atNNNN], e.g. [at0042]. Node identifiers are shown in magenta in this document.
5.2.4. Natural Language
cADL is completely independent of all natural languages. The only potential exception is where constraints include literal values from some language, and this is easily and routinely avoided by the use of separate language and terminology definitions, as used in ADL archetypes. However, for the purposes of readability, comments in English have been included in this document to aid the reader. In real cADL documents, comments are generated from the archetype ontology in the language of the locale.
5.3. Structure
cADL constraints are written in a block-structured style, similar to block-structured programming languages like C. A typical block resembles the following (the recurring pattern /.+/ is a regular expression meaning "non-empty string"):
PERSON[at0001] ∈ {
name ∈ {
PERSON_NAME[at0002] ∈ {
forenames cardinality ∈ {1..*} ∈ {/.+/}
family_name ∈ {/.+/}
title ∈ {"Dr", "Miss", "Mrs", "Mr"}
}
}
addresses cardinality ∈ {1..*} ∈ {
LOCATION_ADDRESS[at0003] ∈ {
street_number existence ∈ {0..1} ∈ {/.+/}
street_name ∈ {/.+/}
locality ∈ {/.+/}
post_code ∈ {/.+/}
state ∈ {/.+/}
country ∈ {/.+/}
}
}
}In the above, an identifier (shown in green in this document) followed by the ∈ operator (equivalent text keyword: matches or is_in ) followed by an open brace, is the start of a 'block', which continues until the closing matching brace (normally visually indented to match the line at the beginning of the block).
The example above expresses a constraint on an instance of the type PERSON; the constraint is expressed by everything inside the PERSON block. The two blocks at the next level define constraints on properties of PERSON, in this case name and addresses. Each of these constraints is expressed in turn by the next level containing constraints on further types, and so on. The general structure is therefore a recursive nesting of constraints on types, followed by constraints on properties (of that type), followed by types (being the types of the attribute under which it appears) until leaf nodes are reached.
We use the term "object" block or node to refer to any block introduced by a type name (in this document, in all upper case), while an "attribute" block or node is any block introduced by an attribute identifier (in all lower case in this document), as illustrated below.
5.3.1. Complex Objects
It may by now be clear that the identifiers in the above could correspond to entities in an object-oriented information model. A UML model compatible with the example above is shown in the following figure. Note that there can easily be more than one model compatible with a given fragment of cADL syntax, and in particular, there may be more properties and classes in the reference model than are mentioned in the cADL constraints. In other words, a cADL text includes constraints only for those parts of a model which are useful or meaningful to constrain.
Constraints expressed in cADL cannot be stronger than those from the information model. For example, the PERSON.family_name attribute is mandatory in the model in the above PERSON model, so it is not valid to express a constraint allowing the attribute to be optional. In general, a cADL archetype can only further constrain an existing information model. However, it must be remembered that for very generic models consisting of only a few classes and a lot of optionality, this rule is not so much a limitation as a way of adding meaning to information. Thus, for a demographic information model which has only the types PARTY and PERSON, one can write cADL which defines the concepts of entities such as COMPANY , EMPLOYEE , PROFESSIONAL , and so on, in terms of constraints on the types available in the information model.
This general approach can be used to express constraints for instances of any information model. The following example shows how to express a constraint on the value property of an ELEMENT class to be a DV_QUANTITY with a suitable range for expressing blood pressure.
ELEMENT[at0010] matches { -- diastolic blood pressure
value matches {
QUANTITY matches {
magnitude matches {|0..1000|}
property matches {"pressure"}
units matches {"mm[Hg]"}
}
}
}5.3.2. Attribute Constraints
In any information model, attributes are either single-valued or multiply-valued, i.e. of a generic container type such as List<Contact>.
5.3.2.1. Existence
The only constraint that applies to all attributes is to do with existence. Existence constraints say whether an attribute value must exist, and are indicated by 0..1 or 1 markers at line ends in UML diagrams (and often mistakenly referred to as a "cardinality of 1..1"). It is the absence or presence of the cardinality constraint in cADL which indicates that the attribute being constrained is single-valued or a container attribute respectively. Existence constraints are expressed in cADL as follows:
QUANTITY matches {
units existence matches {0..1} matches {"mm[Hg]"}
}The meaning of an existence constraint is to indicate whether a value - i.e. an object - is mandatory or optional (i.e. obligatory or not) in runtime data for the attribute in question. The same logic applies whether the attribute is of single or multiple cardinality, i.e. whether it is a container type or not. For container attributes, the existence constraint indicates whether the whole container (usually a list or set) is mandatory or not; a further cardinality constraint (described below) indicates how many members in the container are allowed.
An existence constraint may be used directly after any attribute identifier, and indicates whether the object to which the attribute refers is mandatory or optional in the data.
Existence is shown using the same constraint language as the rest of the archetype definition. Existence constraints can take the values {0} , {0..0} , {0..1} , {1} , or {1..1} . The first two of these constraints may not seem initially obvious, but can be used to indicate that an attribute must not be present in the particular situation modelled by the archetype. The default existence constraint, if none is shown, is {1..1}.
5.3.3. Single-valued Attributes
Repeated blocks of object constraints of the same class (or its subtypes) can have two possible meanings in cADL, depending on whether the cardinality is present or not in the containing attribute block. With no cardinality, the meaning is that each child object constraint of the attribute in question is a possible alternative for the value of the attribute in the data, as shown in the following example:
ELEMENT[at0004] matches { -- speed limit
value matches {
DV_QUANTITY matches { -- miles per hour
magnitude matches {|0..55|}
property matches {"velocity"}
units matches {"mph"}
}
DV_QUANTITY matches { -- km per hour
magnitude matches {|0..100|}
property matches {"velocity"}
units matches {"km/h"}
}
}
}Here, the cardinality of the value attribute is 1..1 (the default), while the occurrences of both QUANTITY constraints is optional, leading to the result that only one QUANTITY instance can appear in runtime data, and it can match either of the constraints.
Two or more object blocks introduced by type names appearing after an attribute which is not a container (i.e. for which there is no cardinality constraint) are taken to be alternative constraints, only one of which needs to be matched by the data.
Note that there is a more efficient way to express the above example, using domain type extensions. See Section 9.
5.3.4. Container Attributes
5.3.4.1. Cardinality
The cardinality of container attributes may be constrained in cADL with the cardinality constraint. Cardinality indicates limits on the number of instance members of a container types such as lists and sets. Consider the following example:
HISTORY occurrences ∈ {1} ∈ {
periodic ∈ {False}
events cardinality ∈ {*} ∈ {
EVENT[at0002] occurrences ∈ {0..1} ∈ { } -- 1 min sample
EVENT[at0003] occurrences ∈ {0..1} ∈ { } -- 2 min sample
EVENT[at0004] occurrences ∈ {0..1} ∈ { } -- 3 min sample
}
}The keyword cardinality implies firstly that the property events must be of a container type, such as List<T> , Set<T> , Bag<T> . The integer range indicates the valid membership of the container; a single * means the range 0..*, i.e. '0 to many'. The type of the container is not explicitly indicated, since it is usually defined by the information model. However, the semantics of a logical set (unique membership, ordering not significant), a logical list (ordered, non-unique membership) or a bag (unordered, non-unique membership) can be constrained using the additional keywords ordered , unordered , unique and non-unique within the cardinality constraint, as per the following examples:
events cardinality ∈ {*; ordered} ∈ { -- logical list
events cardinality ∈ {*; unordered; unique} ∈ { -- logical set
events cardinality ∈ {*; unordered} ∈ { -- logical bagIn theory, none of these constraints can be stronger than the semantics of the corresponding container in the relevant part of the reference model. However, in practice, developers often use lists to facilitate integration, when the actual semantics are intended to be of a set; in such cases, they typically ensure set-like semantics in their own code rather than by using an Set<T> type. How such constraints are evaluated in practice may depend somewhat on knowledge of the software system.
A cardinality constraint may be used after any attribute name (or after its existence constraint, if there is one) in order to indicate that the attribute refers to a container type, what number of member items it must have in the data, and optionally, whether it has "list", "set", or "bag" semantics, via the use of the keywords ordered, unordered, unique and non-unique.
The numeric part of the cardinality contraint can take the values {0}, {0..0}, {0..n}, {m..n}, {0..*}, or {*}, or a syntactic equivalent. The first two of these constraints are unlikely to be useful, but there is no reason to prevent them. There is no default cardinality, since if none is shown, the relevant attribute is assumed to be single-valued (in the interests of uniformity in archetypes, this holds even for smarter parsers that can access the reference model and determine that the attribute is in fact a container).
Cardinality and existence constraints can co-occur, in order to indicate various combinations on a container type property, e.g. that it is optional, but if present, is a container that may be empty, as in the following:
events existence ∈ {0..1} cardinality ∈ {0..*} ∈ {-- etc --}5.3.4.2. Occurrences
A constraint on occurrences is used only with cADL object nodes (not attribute nodes), to indicate how many times in runtime data an instance of a given class conforming to a particular constraint can occur. It only has significance for objects which are children of a container attribute, since by definition, the occurrences of an object which is the value of a single valued attribute can only be 0..1 or 1..1, and this is already defined by the attribute existence. However, it is not illegal. In the example below, three EVENT constraints are shown; the first one ("1 minute sample") is shown as mandatory, while the other two are optional.
In the example below, three EVENT constraints are shown; the first one ("1 minute sample") is shown as mandatory, while the other two are optional.
events cardinality ∈ {*} ∈ {
EVENT[at0002] occurrences ∈ {1..1} ∈ { } -- 1 min sample
EVENT[at0003] occurrences ∈ {0..1} ∈ { } -- 2 min sample
EVENT[at0004] occurrences ∈ {0..1} ∈ { } -- 3 min sample
}Another contrived example below expresses a constraint on instances of GROUP such that for GROUPs representing tribes, clubs and families, there can only be one "head", but there may be many members.
GROUP[iat0103] ∈ {
kind ∈ {/tribe|family|club/}
members cardinality ∈ {*} ∈ {
PERSON[at0104] occurrences ∈ {1} ∈ {
title ∈ {"head"}
-- etc --
}
PERSON[at0105] occurrences ∈ {0..*} ∈ {
title ∈ {"member"}
-- etc --
}
}
}The first occurrences constraint indicates that a PERSON with the title "head" is mandatory in the GROUP, while the second indicates that at runtime, instances of PERSON with the title "member" can number from none to many. Occurrences may take the value of any range including {0..*}, meaning that any number of instances of the given type may appear in data, each conforming to the one constraint block in the archetype. A single positive integer, or the infinity indicator, may also be used on its own, thus: {2}, {*}. A range of {0..0} or {0} indicates that no occurrences of this object are allowed in this archetype. The default occurrences, if none is mentioned, is {1..1}.
An occurrences constraint may appear directly after the type name of any object constraint within a container attribute, in order to indicate how many times data objects conforming to the block introduced by the type name may occur in the data.
Where cardinality constraints are used (remembering that occurrences is always there by default, if not explicitly specified), cardinality and occurrences must always be compatible. The validity rule is:
VCOC: cardinality/occurrences validity: the interval represented by: (the sum of all occurrences minimum values) .. (the sum of all occurrences maximum values) must be inside the interval of the cardinality.
5.3.5. "Any" Constraints
There are two cases where it is useful to state a completely open, or "any", constraint. The "any" constraint is shown by a single asterisk (*) in braces. The first is when it is desired to show explicitly that some property can have any value, such as in the following:
PERSON[at0001] ∈ {
name existence ∈ {0..1} matches {*}
-- etc --
}The "any" constraint on name means that any value permitted by the underlying information model is also permitted by the archetype; however, it also provides an opportunity to specify an existence constraint which might be narrower than that in the information model. If the existence constraint is the same, an "any" constraint on a property is equivalent to no constraint being stated at all for that property in the cADL.
The second use of "any" as a constraint value is for types, such as in the following:
ELEMENT[at0004] ∈ { -- speed limit
value ∈ {
QUANTITY matches {*}
}
}The meaning of this constraint is that in the data at runtime, the value property of ELEMENT must be of type QUANTITY, but can have any value internally. This is most useful for constraining objects to be of a certain type, without further constraining value, and is especially useful where the information model contains subtyping, and there is a need to restrict data to be of certain subtypes in certain contexts.
5.3.6. Object Node Identification and Paths
In many of the examples above, some of the object node typenames are followed by a node identifier, shown in brackets.
Node identifiers are required for any object node which is intended to be addressable elsewhere in the cADL text, or in the runtime system and which would otherwise be ambiguous i.e. has sibling nodes.
In the following example, the PERSON type does not require an identifier, since no sibling node exists at the same level, and unambigous paths can be formed:
members cardinality ∈ {*} ∈ {
PERSON ∈ {
title ∈ {"head"}
}
}The path to the title attribute is members/title However, where there are more than one sibling node, node identifiers must be used to ensure distinct paths:
members cardinality ∈ {*} ∈ {
PERSON[at0104] ∈ {
title ∈ {"head"}
}
PERSON[at0105] matches {
title ∈ {"member"}
}
}The paths to the respective title attributes are now:
members[at0104]/title
members[at0105]/titleLogically, all non-unique parent nodes of an identified node must also be identified back to the root node. The primary function of node identifiers is in forming paths, enabling cADL nodes to be unambiguously referred to. The node identifier can also perform a second function, that of giving a design-time meaning to the node, by equating the node identifier to some description. Thus, in the example shown in Section 5.3.1, the ELEMENT node is identified by the code [at0010], which can be designated elsewhere in an archetype as meaning "diastolic blood pressure".
Node ids are required only where it is necessary to create paths, for example in use_node statements. However, the underlying reference model might have stronger requirements. The openEHR Reference Model for example requires that all node types which inherit from the class LOCATABLE have both a archetype_node_id and a runtime name attribute. Only data types (such as QUANTITY, CODED_TEXT) and their constituent types are exempt.
Paths are used in cADL to refer to cADL nodes, and are expressed in the ADL path syntax, described in detail in Section 7. ADL paths have the same alternating object/attribute structure implied in the general hierarchical structure of cADL, obeying the pattern TYPE/attribute/TYPE/attribute/….
Paths in cADL always refer to object nodes, and can only be constructed through nodes having node ids, or nodes which are the only child object of a single-cardinality attribute.
Unusually for a path syntax, a trailing object identifier can be required, even if the attribute corresponds to a single relationship (as might be expected with the "name" property of an object) because in cADL, it is legal to define multiple alternative object constraints - each identified by a unique node id - for a relationship node which has single cardinality.
Consider the following cADL example:
HISTORY occurrences ∈ {1} ∈ {
periodic ∈ {False}
events cardinality ∈ {*} ∈ {
EVENT[at0002] occurrences ∈ {0..1} ∈ { } -- 1 min sample
EVENT[at0003] occurrences ∈ {0..1} ∈ { } -- 2 min sample
EVENT[at0004] occurrences ∈ {0..1} ∈ { } -- 3 min sample
}
}The following paths can be constructed:
/ -- the HISTORY (root) object
/periodic -- the HISTORY.periodic attribute
/events[at0002] -- the 1 minute event object
/events[at0003] -- the 2 minute event object
/events[at0004] -- the 3 minute event objectIt is valid to add attribute references to the end of a path, if the underlying information model permits it, as in the following example.
/events/count -- count attribute of the items propertyThe examples above are physical paths because they refer to object nodes using codes. Physical paths can be rendered as logical paths using descriptive meanings for node identifiers, if defined. Thus, the following two paths might be equivalent:
/events[at0004] -- the 3 minute event object
/events[3 minute event] -- the 3 minute event object
None of the paths shown here have any validity outside the cADL block in which they occur, since they do not include an identifier of the enclosing document, normally an archetype. To reference a cADL node in a document from elsewhere (e.g. another archetype of a template) requires that the identifier of the document itself be prefixed to the path, as in the following archetype example:
[openehr-ehr-entry.apgar-result.v]/events[at0001]
This kind of path expression is necessary to form the paths that occur when archetypes are composed to form larger structures.
5.3.7. Internal References
It occurs reasonably often that one needs to include a constraint which is a repeat of an earlier complex constraint, but within a different block. This is achieved using an archetype internal reference, according to the following rule:
An archetype internal reference is introduced with the use_node keyword, in a line of the following form:
use_node TYPE object_path
This statement says: use the node of type TYPE, found at (the existing) path object_path. The following example shows the definitions of the ADDRESS nodes for phone, fax and email for a home CONTACT being reused for a work CONTACT.
PERSON ∈ {
identities ∈ {
-- etc --
}
contacts cardinality ∈ {0..*} ∈ {
CONTACT[at0002] ∈ { -- home address
purpose ∈ {...}
addresses ∈ {...}
}
CONTACT[at0003] ∈ { -- postal address
purpose ∈ {...}
addresses ∈ {...}
}
CONTACT[at0004] ∈ { -- home contact
purpose ∈ {...}
addresses cardinality ∈ {0..*} ∈ {
ADDRESS[at0005] ∈ { -- phone
type ∈ {...}
details ∈ {...}
}
ADDRESS[at0006] ∈ { -- fax
type ∈ {...}
details ∈ {...}
}
ADDRESS[at0007] ∈ { -- email
type ∈ {...}
details ∈ {...}
}
}
}
CONTACT[at0008] ∈ { -- work contact
purpose ∈ {...}
addresses cardinality ∈ {0..*} ∈ {
use_node ADDRESS /contacts[at0004]/addresses[at0005] -- phone
use_node ADDRESS /contacts[at0004]/addresses[at0006] -- fax
use_node ADDRESS /contacts[at0004]/addresses[at0007] -- email
}
}
}
}The type mentioned in the use_node reference must always be the same type as, or a super-type of the referenced type. In most cases, it will be the same. In some cases, an archetype section might use a subtype of the type required by the reference model (e.g. in the above example, a type such as POSTAL_ADDRESS); a use_node reference to such a node can legally mention the parent type (ADDRESS, in the example). Whether this possibility has practical utility remains to be seen.
VUNT: use_node type: the type mentioned in a use_node must be the same as or a super-type (according to the reference model) of the reference model type of the node referred to.
Like any other object node, a node defined using an internal reference has occurrences. Unlike other node types, if no occurrences is mentioned, the value of the occurrences is set to that of the referenced node (which if not explicitly mentioned will be the default occurrences). However, the occurrences can be overridden in the referring node as well, as in the following example which enables the specification for 'phone' to be re-used, but with a different occurrences constraint.
PERSON[at0000] ∈ {
contacts cardinality ∈ {0..*} ∈ {
CONTACT[at0004] ∈ { -- home contact
addresses cardinality ∈ {0..*} ∈ {
ADDRESS[at0005] occurrences ∈ {1} ∈ { ...} -- phone
}
}
CONTACT[at0008] ∈ { -- work contact
addresses cardinality ∈ {0..*} ∈ {
use_node ADDRESS[at0009] occurrences ∈ {0..*} /contacts[at0004]/addresses[at0005] -- phone
}
}
}
}5.3.8. Archetype Slots
At any point in a cADL definition, a constraint can be defined that allows other archetypes to be used, rather than defining the desired constraints inline. This is known as an archetype 'slot' or 'chaining point', i.e. a connection point whose allowable 'fillers' are constrained by a set of statements, written in the ADL assertion language (described in Section 6).
An archetype slot is defined in terms of two lists of assertions statements defining which archetypes are allowed and/or which are excluded from filling that slot.
An archetype slot is introduced with the keyword allow_archetype, and is expressed using two lists of assertions, introduced with the keywords include and exclude, respectively.
Since archetype slots are typed, the (possibly abstract) type of the allowed archetypes is already constrained. Otherwise, any assertion about a filler archetype can be made. The assertions do not constrain data in the way that other archetype statements do, instead they constrain archetypes. Two kinds of reference may be used in a slot assertion. The first is a reference to an object-oriented property of the filler archetype itself, where the property names are defined by the ARCHETYPE class in the Archetype Object Model. Examples include:
archetype_id parent_archetype_id short_concept_name
This kind of reference is usually used to constrain the allowable archetypes based on archetype_id or some other meta-data item (e.g. archetypes written in the same organisation). The second kind of reference is to absolute paths in the definition section of the filler archetype (i.e. 'archetype paths' as used throughout this section of the specification). Both kinds of reference take the form of an Xpath-style path, with the distinction that paths referring to ARCHETYPE attributes not in the definition section do not start with a slash (this allows parsers to easily distinguish the two types of reference).
5.3.8.1. Defining Slots on the basis of Archetype Identifiers and Concepts
A basic kind of assertion is on the identifier of archetypes allowed in the slot. This is achieved with statements like the following in the include and exclude lists:
archetype_id ∈ {/.*\.SECTION\..*\..*/} -- match any SECTION archetypeIt is possible to limit valid slot-fillers to a single archetype simply by stating a full archetype identifier with no wildcards; this has the effect that the choice of archetype in that slot is predetermined by the archetype and cannot be changed later. In general, however, the intention of archetypes is to provide highly re-usable models of real world content with local constraining left to templates, in which case a 'wide' slot definition is used (i.e. matches many possible archetypes).
The following example shows how the "Objective" SECTION in a problem/SOAP headings archetype defines two slots, indicating which OBSERVATION and SECTION archetypes are allowed and excluded under the items property.
SECTION [at2000] occurrences ∈ {0..1} ∈ { -- objective
items cardinality ∈ {0..*} ∈ {
allow_archetype OBSERVATION occurrences ∈ {0..1} ∈ {
include
short_concept_name ∈ {/.+/}
}
allow_archetype SECTION occurrences ∈ {0..*} ∈ {
include
archetype_id/value ∈ {/.*/}
exclude
archetype_id/value ∈ {/openEHR-EHR-SECTION\.patient_details\..+/}
}
}
}Here, every constraint inside the block starting on an allow_archetype line contains constraints that must be met by archetypes in order to fill the slot. In the examples above, the constraints are in the form of regular expressions on archetype identifiers. In cADL, the PERL regular expression syntax is assumed.
5.3.8.2. Using Other Constraints in Slots
Other constraints are possible as well, including that the allowed archetype must contain a certain keyword, or a certain path. The latter allows archetypes to be linked together on the basis of content. For example, under a "genetic relatives" heading in a Family History Organiser archetype, the following slot constraint might be used:
allow_archetype EVALUATION occurrences ∈ {0..*} matches {
include
short_concept_name ∈ {"risk_family_history"}
∧ ∃ /subject/relationship/defining_code -> ~ /subject/relationship/defining_code/code_list.has([openehr::0]) -- self
}This says that the slot allows archetypes on the EVALUATION class, which either have as their concept "risk_family_history" or, if there is a constraint on the subject relationship, then it may not include the code [openehr::0] (the openEHR term for "self") - i.e. it must be an archetype designed for family members rather than the subject of care herself.
5.3.9. Placeholder Constraints
Not all constraints can be defined easily within an archetype. One common category of constraint that should be defined externally, and referenced from the archetype is the 'value set' for a coded attribute. The need within the archetype in this case is to limit an attribute value to a particular set of codes, i.e. value set, from a terminology.
The value set could be simply enumerated within the archetype, for example using the C_CODE_PHRASE type defined in the openEHR Archetype Profile; this will work perfectly well, but has at least two limitations. Firstly, the intended set of values allowed for the attribute may change over time (e.g. as has happened with 'types of hepatitis' since 1980), requiring the archetype to be updated. With a large repository of archetypes, each containing coded term constraints, this approach is likely to be unsustainable and error-prone. Secondly, the best means of defining the value set is in general not likely to be via enumeration of the individual terms, but in the form of a semantic expression that can be evaluated against the terminology. This is because the value set is typically logically specified in terms of inclusions, exclusions, conjunctions and disjunctions of general categories.
Consider for example the value set logically defined as "any bacterial infection of the lung". The possible values would be codes from a target terminology, corresponding to numerous strains of pneumococcus, staphlycoccus and so on, but not including species that are never found in the lung. Rather than enumerate the list of codes corresponding to this value set (which is likely to be quite large), the archetype author is more likely to rely on semantic links within the terminology to express the set; a query such as 'is-a bacteria and has-site lung' might be definable against the terminology (such as SNOMED CT or the WHO ICD10 terminology).
In a similar way, other value sets, including for quantitative values, are likely to be specified by queries or formal expressions, and evaluated by an external knowledge service. Examples include "any unit of pressure" and "normal range values for serum sodium".
In all such cases, expressing the constraint could be done by including the query or other formal expression within the archetype itself. However, experience shows that this is problematic in various ways. Firstly, there is little if any standardisation in such formal value set expressions or queries for use with knowledge services; two archetype authors could easily create competing syntactical expressions for the same logical constraint. A second problem is that errors might be made in the query expression itself, or the expression may be correct at the time of authoring, but need subsequent adjustment as the relevant knowledge resource grows and changes. The consequence of this is the same as for a value set enumerated inline - it is unlikely to be sustainable for large numbers of archetyes. These problems are not accidental: a query with respect to a terminological, ontological or other knowledge resource is most likely to be authored correctly by maintainers or experts of the knowledge resource, rather than archetype authors; it may well be altered over time due to improvements in the query formalism itself.
The solution adopted in ADL is to store only identifiers of query expressions which when evaluated return a required value set, while query expressions are assumed to be stored in a query repository, or some part of the relevant knowedge service. Rather than store external identifiers inline in a cADL text, the ADL approach is to store a 'placeholder' internal code of the form [acNNNN], e.g. [ac0012]. Codes of this form are defined in the archetype ontology section, and can be mapped to query identifiers for one or more knowledge resources. This approach would allow a single 'ac' code to be defined for the value set.
5.3.10. Mixed Structures
Three types of structure representing constraints on complex objects have been presented so far:
-
complex object structures: any node introduced by a type name and followed by {} containing constraints on attributes;
-
internal references: any node introduced by the keyword use_node, followed by a type name; such nodes indicate re-use of a complex object constraint that has already been expressed elsewhere in the archetype;
-
archetype slots: any node introduced by the keyword allow_archetype, followed by a type name; such nodes indicate a complex object constraint which is expressed in some other archetype.
At any given node, all three types can co-exist, as in the following example:
SECTION[at2000] ∈ {
items cardinality ∈ {0..*; ordered} ∈ {
ENTRY[at2001] ∈ {...}
allow_archetype ENTRY[at2002] ∈ {...}
use_node ENTRY[at2003] /some_path[at0004]
ENTRY[at2004] ∈ {...}
use_node ENTRY[at2005] /some_path[at1012]
use_node ENTRY[at2006] /some_path[at1052]
ENTRY[at2007] ∈ {...}
}
}Here we have a constraint on an attribute called items (of cardinality 0..*), expressed as a series of possible constraints on objects of type ENTRY. The 1st, 4th and 7th are described inline; the 3rd, 5th and 6th are expressed in terms of internal references to other nodes earlier in the archetype, while the 2nd is an archetype slot, whose constraints are expressed in other archetypes matching the include/exclude constraints appearing between the braces of this node. Note also that the ordered keyword on the enclosing items node has been used to indicate that the list order is intended to be significant.
5.4. Constraints on Primitive Types
While constraints on complex types follow the rules described so far, constraints on attributes of primitive types in cADL are expressed without type names, and omitting one level of braces, as follows:
some_attr matches {some_pattern}rather than:
some_attr matches {
PRIMITIVE_TYPE matches {
some_pattern
}
}This is made possible because the syntax patterns of all primitive type constraints are mutually distinguishable, i.e. the type can always be inferred from the syntax alone. Since all leaf attributes of all object models are of primitive types, or lists or sets of them, cADL archetypes using the brief form for primitive types are significantly less verbose overall, as well as being more directly comprehensible to human readers. Currently the cADL grammar only supports the brief form used in this specification since no practical reason has been identified for supporting the more verbose version. Theoretically however, there is nothing to prevent it being used in the future, or in some specialist application.
5.4.1. Constraints on String
Strings can be constrained in two ways: using a list of fixed strings, and using using a regular expression. All constraints on strings are case-sensitive.
5.4.1.1. List of Strings
A String-valued attribute can be constrained by a list of strings (using the dADL syntax for string lists), including the simple case of a single string. Examples are as follows:
species ∈ {"platypus"}
species ∈ {"platypus", "kangaroo"}
species ∈ {"platypus", "kangaroo", "wombat"}The first example constrains the runtime value of the species attribute of some object to take the value "platypus"; the second constrains it be either "platypus" or "kangaroo", and so on. In almost all cases, this kind of string constraint should be avoided, since it usually renders the body of the archetype language-dependent. Exceptions are proper names (e.g. "NHS", "Apgar"), product tradenames (but note even these are typically different in different language locales, even if the different names are not literally translations of each other). The preferred way of constraining string attributes in a language independent way is with local [ac] codes. See Section 8.2.3.
5.4.1.2. Regular Expression
The second way of constraining strings is with regular expressions, a widely used syntax for expressing patterns for matching strings. The regular expression syntax used in cADL is a proper subset of that used in the Perl language (see [Perl_regex] for a full specification of the regular expression language of Perl). It is specified as a constraint using either // or ^^ delimiters:
string_attr matches {/regular expression/}
string_attr matches {=~ /regular expression}
string_attr matches {!~ /regular expression}The first two are identical, indicating that the attribute value must match the supplied regular expression. The last indicates that the value must not match the expression. If the delimiter character is required in the pattern, it must be quoted with the backslash ('\') character, or else alternative delimiters can be used, enabling more comprehensible patterns. A typical example is regular expressions including units. The following two patterns are equivalent:
units ∈ {/km\/h|mi\/h/}
units ∈ {^km/h|mi/h^}The rules for including special characters within strings are described in Section 3.
The regular expression patterns supported in cADL are as follows.
| Atomic Items | ||
|---|---|---|
|
match any single character. |
E.g. |
|
match any of the characters in the set |
E.g. |
|
match any of the characters in the set of characters formed by the continuous range from |
E.g. |
|
match any character except those in the set of characters formed by the continuous range from |
E.g. |
Grouping |
||
|
parentheses are used to group items; any pattern appearing within parentheses is treated as an atomic item for the purposes of the occurrences operators. |
E.g. |
Occurrences |
||
|
match 0 or more of the preceding atomic item. |
E.g. |
|
match 1 or more occurrences of the preceding atomic item. |
E.g. |
|
match 0 or 1 occurrences of the preceding atomic item. |
E.g. |
|
match m to n occurrences of the preceding atomic item. |
E.g. |
|
match at least m occurrences of the preceding atomic item; |
|
|
match at most n occurrences of the preceding atomic item; |
|
|
match exactly m occurrences of the preceding atomic item; |
|
Special Character Classes |
||
|
match a decimal digit character; match a non-digit character; |
|
|
match a whitespace character; match a non-whitespace character; |
|
Alternatives |
||
|
match either pattern1 or pattern2. |
E.g. |
A similar warning should be noted for the use of regular expressions to constrain strings: they should be limited to non-linguistically dependent patterns, such as proper and scientific names. The use of regular expressions for constraints on normal words will render an archetype linguistically dependent, and potentially unusable by others.
5.4.2. Constraints on Integer
Integers can be constrained using a list of integer values, and using an integer interval.
5.4.2.1. List of Integers
Lists of integers expressed in the syntax from ODIN can be used as a constraint, e.g.:
length matches {1000} -- fixed value of 1000
magnitude matches {0, 5, 8} -- any of 0, 5 or 8The first constraint requires the attribute length to be 1000, while the second limits the value of magnitude to be 0, 5, or 8 only.
5.4.2.2. Interval of Integer
Integer intervals are expressed using the interval syntax from dADL (described in the dADL specification). Examples of 2-sided intervals include:
length matches {|1000|} -- point interval of 1000 (=fixed value)
length matches {|950..1050|} -- allow 950 - 1050
length matches {|0..1000|} -- allow 0 - 1000
length matches {|0..<1000|} -- allow 0>= x <1000
length matches {|0>..<1000|} -- allow 0> x <1000
length matches {|100+/-5|} -- allow 100 +/- 5, i.e. 95 - 105
rate matches {|0..infinity|} -- allow 0 - infinity, i.e. same as >= 0Examples of one-sided intervals include:
length matches {|<10|} -- allow up to 9
length matches {|>10|} -- allow 11 or more
length matches {|<=10|} -- allow up to 10
length matches {|>=10|} -- allow 10 or more5.4.3. Constraints on Real
Constraints on Real values follow exactly the same syntax as for Integers, in both list and interval forms. The only difference is that the real number values used in the constraints are indicated by the use of the decimal point and at least one succeeding digit, which may be 0. Typical examples are:
magnitude ∈ {5.5} -- list of one (fixed value)
magnitude ∈ {|5.5|} -- point interval (=fixed value)
magnitude ∈ {|5.5..6.0|} -- interval
magnitude ∈ {5.5, 6.0, 6.5} -- list
magnitude ∈ {|0.0..<1000.0|} -- allow 0>= x <1000.0
magnitude ∈ {|<10.0|} -- allow anything less than 10.0
magnitude ∈ {|>10.0|} -- allow greater than 10.0
magnitude ∈ {|<=10.0|} -- allow up to 10.0
magnitude ∈ {|>=10.0|} -- allow 10.0 or more
magnitude ∈ {|80.0+/-12.0|} -- allow 80 +/- 125.4.4. Constraints on Boolean
Boolean runtime values can be constrained to be True, False, or either, as follows:
some_flag matches {True}
some_flag matches {False}
some_flag matches {True, False}5.4.5. Constraints on Character
Characters can be constrained in two ways: using a list of characters, and using a regular expression.
5.4.5.1. List of Characters
The following examples show how a character value may be constrained using a list of fixed character values. Each character is enclosed in single quotes.
color_name matches {'r'}
color_name matches {'r', 'g', 'b'}5.4.5.2. Regular Expression
Character values can also be constrained using a single-character regular expression character class, as per the following examples:
color_name matches {/[rgbcmyk]/}
color_name matches {/[^\s\t\n]/}The only allowed elements of the regular expression syntax in character expressions are the following:
-
any item from the Character Classes list above;
-
any item from the Special Character Classes list above;
-
an alternative expression whose parts are any item types, e.g.
'a'|'b'|[m-z]
5.4.6. Constraints on Dates, Times and Durations
Dates, times, date/times and durations may all be constrained in three ways: using a list of values, using intervals, and using patterns. The first two ways allow values to be constrained to actual date, time etc values, while the last allows values to be constrained on the basis of which parts of the date, time etc are present or missing, regardless of value. The pattern method is described first, since patterns can also be used in lists and intervals.
5.4.6.1. Date, Time and Date/Time
Patterns
Dates, times, and date/times (i.e. timestamps), can be constrained using patterns based on the ISO 8601 date/time syntax, which indicate which parts of the date or time must be supplied. A constraint pattern is formed from the abstract pattern yyyy-mm-ddThh:mm:ss (itself formed by translating each field of an ISO 8601 date/time into a letter representing its type), with either ? (meaning optional) or X (not allowed) characters substituted in appropriate places. The syntax of legal patterns is shown by the following lexical rules:
DATE_CONSTRAINT_PATTERN : YEAR_PATTERN '-' MONTH_PATTERN '-' DAY_PATTERN ;
TIME_CONSTRAINT_PATTERN : HOUR_PATTERN ':' MINUTE_PATTERN ':' SECOND_PATTERN ;
DATE_TIME_CONSTRAINT_PATTERN : DATE_CONSTRAINT_PATTERN 'T' TIME_CONSTRAINT_PATTERN ;
// date time pattern
fragment YEAR_PATTERN : ( 'yyy' 'y'? ) | ( 'YYY' 'Y'? ) ;
fragment MONTH_PATTERN : 'mm' | 'MM' | '??' | 'XX' | 'xx' ;
fragment DAY_PATTERN : 'dd' | 'DD' | '??' | 'XX' | 'xx' ;
fragment HOUR_PATTERN : 'hh' | 'HH' | '??' | 'XX' | 'xx' ;
fragment MINUTE_PATTERN : 'mm' | 'MM' | '??' | 'XX' | 'xx' ;
fragment SECOND_PATTERN : 'ss' | 'SS' | '??' | 'XX' | 'xx' ;All expressions generated by these patterns must also satisfy the validity rules:
-
where
??appears in a field, only??orXXcan appear in fields to the right -
where
XXappears in a field, onlyXXcan appear in fields to the right
The following table shows the valid patterns that can be used, and the types implied by each pattern.
| Implied Type | Pattern | Explanation |
|---|---|---|
Date |
yyyy-mm-dd |
full date must be specified |
Date |
yyyy-mm-?? |
optional day; |
Date |
yyyy-??-?? |
optional month, optional day; |
Date |
yyyy-mm-XX |
mandatory month, no day |
Date |
yyyy-??-XX |
optional month, no day |
|
|
|
Time |
hh:mm:ss |
full time must be specified |
Time |
hh:mm:XX |
no seconds; |
Time |
hh:??:XX |
optional minutes, no seconds; |
Time |
hh:??:?? |
optional minutes, seconds; |
|
|
|
Date/Time |
yyyy-mm-ddThh:mm:ss |
full date/time must be specified |
Date/Time |
yyyy-mm-ddThh:mm:?? |
optional seconds; |
Date/Time |
yyyy-mm-ddThh:mm:XX |
no seconds; |
Date/Time |
yyyy-mm-ddThh:??:XX |
no seconds, minutes optional; |
Date/Time |
yyyy-??-??T??:??:?? |
minimum valid date/time constraint |
In the above patterns, the 'yyyy' etc match strings can be replaced by literal date/time numbers. For example, yyyy-??-XX could be transformed into 1995-??-XX to mean any partial date in 1995.
An assumed value can be used with any of the above as follows: yyyy-??-??; 1970-01-01.
Intervals
Dates, times and date/times can also be constrained using intervals. Each date, time etc in an interval may be a literal date, time etc value. Examples of such constraints:
|1995-??-XX| -- any partial date in 199
|09:30:00| -- exactly 9:30 am
|< 09:30:00| -- any time before 9:30 am
|<= 09:30:00| -- any time at or before 9:30 am
|> 09:30:00| -- any time after 9:30 am
|>= 09:30:00| -- any time at or after 9:30 am
|2004-05-20..2004-06-02| -- a date range
|2004-05-20T00:00:00..2005-05-19T23:59:59| -- a date/time range5.4.6.2. Duration Constraints
Patterns
Patterns based on ISO 8601 can be used to constraint durations in the same way as for Date/time types. The lexical rule for the pattern is:
DURATION_CONSTRAINT_PATTERN : 'P' [yY]?[mM]?[Ww]?[dD]? ( 'T' [hH]?[mM]?[sS]? )? ;|
Note
|
allowing the 'W' designator to be used with the other designators corresponds to a deviation from the published ISO 8601 standard used in openEHR, namely: durations are supposed to take the form of PnnW or PnnYnnMnnDTnnHnnMnnS, but in openEHR, the 'W' (week) designator can be used with the other designators, since it is very common to state durations of pregnancy as some combination of weeks and days.
|
The use of this pattern indicates which 'slots' in an ISO duration string may be filled. Where multiple letters are supplied in a given pattern, the meaning is 'or', i.e. any one or more of the slots may be supplied in the data. This syntax allows specifications like the following to be made:
Pd -- a duration containing days only, e.g. P5d
Pm -- a duration containing months only, e.g. P5m
PTm -- a duration containing minutes only, e.g. PT5m
Pwd -- a duration containing weeks and/or days only, e.g. P4w
PThm -- a duration containing hours and/or minutes only, e.g. PT2h30mLists and Intervals
Durations can also be constrained by using absolute ISO 8601 duration values, or ranges of the same, e.g.:
PT1m -- 1 minute
P1dT8h -- 1 day 8 hrs
|PT0m..PT1m30s| -- Reasonable time offset of first apgar sampleMixed Pattern and Interval
In some cases there is a need to be able to limit the allowed units as well as state a duration interval. This is common in obstetrics, where physicians want to be able to set an interval from say 0-50 weeks and limit the units to only weeks and days. This can be done as follows:
PWD/|P0W..P50W| -- 0-50 weeks, expressed only using weeks and days
The general form is a pattern followed by a slash ('/') followed by an interval, as follows:
duration_constraint: duration_pattern '/' duration_interval ;5.4.7. Constraints on Lists of Primitive types
In many cases, the type in the information model of an attribute to be constrained is a list or set of primitive types, e.g. List<Integer>, Set<String> etc. As for complex types, this is indicated in cADL using the cardinality keyword, as follows:
some_attr cardinality ∈ {0..*} ∈ {some_constraint}The pattern to match in the final braces will then have the meaning of a list or set of value constraints, rather than a single value constraint. Any constraint described above for single-valued attributes, which is commensurate with the type of the attribute in question, may be used. However, as with complex objects, the meaning is now that every item in the list is constrained to be any one of the values implied by the constraint expression. For example,
speed_limits cardinality ∈ {0..*; ordered} ∈ {50, 60, 70, 80, 100, 130}constrains each value in the list corresponding to the value of the attribute speed_limits (of type List<Integer> ), to be any one of the values 50, 60, 70 etc.
5.4.8. Assumed Values
When archetypes are defined to have optional parts, an ability to define 'assumed' values is useful. For example, an archetype for the concept 'blood pressure measurement' might include an optional data point describing the patient position, with choices 'lying', 'sitting' and 'standing'. Since the section is optional, data could be created according to the archetype which does not contain the protocol section. However, a blood pressure cannot be taken without the patient in some position, so clearly there could be an implied or 'assumed' value.
The archetype allows this to be explicitly stated so that all users/systems know what value to assume when optional items are not included in the data. Assumed values are currently definable on primitive types only, and are expressed after the constraint expression, by a semi-colon (';') followed by a value of the same type as that implied by the preceding part of the constraint. The use of assumed values is illustrated here for a number of primitive types:
length matches {|0..1000|; 200} -- allow 0 - 1000, assume 200
some_flag matches {True, False; True} -- allow T or F, assume T
some_date matches {yyyy-mm-dd hh:mm:XX; 1800-01-01T00:00:00}If no assumed value is stated, no reliable assumption can be made by the receiver of the archetyped data about what the values of removed optional parts might be, from inspecting the archetype. However, this usually corresponds to a situation where the assumed value does not even need to be stated - the same value will be assumed by all users of this data, if its value is not transmitted. In other cases, it may be that it doesn’t matter what the assumed value is. For example, an archetype used to capture physical measurements might include a "protocol" section, which in turn can be used to record the "instrument" used to make a given measurement. In a blood pressure specialisation of this archetype it is fairly likely that physicians recording or receiving the data will not care about what instrument was used.
5.5. Syntax Specification
The grammar for the standard cADL syntax is shown below. The form used in openEHR is the same as this, but with custom additions, described in the openEHR Archetype Profile. The resulting grammar and lexical analysis specification used in the openEHR reference ADL parser is implemented using lex (.l file) and yacc (.y file) specifications for the Eiffel programming environment. The current release of these files is available at in the ADL Workbench cADL parser source code. The .l and .y files can be converted for use in other yacc/lex-based programming environments. The production rules of the .y file are available as an HTML document.
5.5.1. Grammar
The following is an extract of the cADL parser production rules (yacc specification). Note that because of interdependencies with path and assertion production rules, practical implementations may have to include all production rules in one parser.
input:
c_complex_object
;
c_complex_object:
c_complex_object_head SYM_MATCHES SYM_START_CBLOCK c_complex_object_body SYM_END_CBLOCK
;
c_complex_object_head:
c_complex_object_id c_occurrences
;
c_complex_object_id:
type_identifier
| type_identifier V_LOCAL_TERM_CODE_REF
;
c_complex_object_body:
c_any
| c_attributes
;
c_object:
c_complex_object
| archetype_internal_ref
| archetype_slot
| constraint_ref
| c_primitive_object
| V_C_DOMAIN_TYPE
;
archetype_internal_ref:
SYM_USE_NODE type_identifier c_occurrences object_path
;
archetype_slot:
c_archetype_slot_head SYM_MATCHES SYM_START_CBLOCK c_includes c_excludes
SYM_END_CBLOCK
;
c_archetype_slot_head:
c_archetype_slot_id c_occurrences
;
c_archetype_slot_id:
SYM_ALLOW_ARCHETYPE type_identifier
| SYM_ALLOW_ARCHETYPE type_identifier V_LOCAL_TERM_CODE_REF
;
c_primitive_object:
c_primitive
;
c_primitive:
c_integer
| c_real
| c_date
| c_time
| c_date_time
| c_duration
| c_string
| c_boolean
;
c_any:
'*'
;
c_attributes:
c_attribute
| c_attributes c_attribute
;
c_attribute:
c_attr_head SYM_MATCHES SYM_START_CBLOCK c_attr_values SYM_END_CBLOCK
;
c_attr_head:
V_ATTRIBUTE_IDENTIFIER c_existence
| V_ATTRIBUTE_IDENTIFIER c_existence c_cardinality
;
c_attr_values:
c_object
| c_attr_values c_object
| c_any
;
c_includes:
// nothing OK
| SYM_INCLUDE assertions
;
c_excludes:
// nothing OK
| SYM_EXCLUDE assertions
;
c_existence:
// nothing OK
| SYM_EXISTENCE SYM_MATCHES SYM_START_CBLOCK existence_spec SYM_END_CBLOCK
;
existence_spec:
V_INTEGER
| V_INTEGER SYM_ELLIPSIS V_INTEGER
;
c_cardinality:
SYM_CARDINALITY SYM_MATCHES SYM_START_CBLOCK cardinality_spec
SYM_END_CBLOCK
;
cardinality_spec:
occurrence_spec
| occurrence_spec ';' SYM_ORDERED
| occurrence_spec ';' SYM_UNORDERED
| occurrence_spec ';' SYM_UNIQUE
| occurrence_spec ';' SYM_ORDERED ';' SYM_UNIQUE
| occurrence_spec ';' SYM_UNORDERED ';' SYM_UNIQUE
| occurrence_spec ';' SYM_UNIQUE ';' SYM_ORDERED
| occurrence_spec ';' SYM_UNIQUE ';' SYM_UNORDERED
;
cardinality_limit_value:
integer_value
| '*'
;
c_occurrences:
// nothing OK
| SYM_OCCURRENCES SYM_MATCHES SYM_START_CBLOCK occurrence_spec SYM_END_CBLOCK
;
occurrence_spec:
cardinality_limit_value
| V_INTEGER SYM_ELLIPSIS cardinality_limit_value
;
c_integer_spec:
integer_value
| integer_list_value
| integer_interval_value
| occurrence_spec
;
c_integer:
c_integer_spec
| c_integer_spec ';' integer_value
;
c_real_spec:
real_value
| real_list_value
| real_interval_value
;
c_real:
c_real_spec
| c_real_spec ';' real_value
;
c_date_constraint:
V_ISO8601_DATE_CONSTRAINT_PATTERN
| date_value
| date_interval_value
;
c_date:
c_date_constraint
| c_date_constraint ';' date_value
;
c_time_constraint:
V_ISO8601_TIME_CONSTRAINT_PATTERN
| time_value
| time_interval_value
;
c_time:
c_time_constraint
| c_time_constraint ';' time_value
;
c_date_time_constraint:
V_ISO8601_DATE_TIME_CONSTRAINT_PATTERN
| date_time_value
| date_time_interval_value
;
c_date_time:
c_date_time_constraint
| c_date_time_constraint ';' date_time_value
;
c_duration_constraint:
duration_pattern
| duration_pattern '/' duration_interval_value
| duration_value
| duration_interval_value
;
duration_pattern:
V_ISO8601_DURATION_CONSTRAINT_PATTERN
;
c_duration:
c_duration_constraint
| c_duration_constraint ';' duration_value
;
c_string_spec:
V_STRING
| string_list_value
| string_list_value ',' SYM_LIST_CONTINUE
| V_REGEXP
;
c_string:
c_string_spec
| c_string_spec ';' string_value
;
c_boolean_spec:
SYM_TRUE
| SYM_FALSE
| SYM_TRUE ',' SYM_FALSE
| SYM_FALSE ',' SYM_TRUE
;
c_boolean:
c_boolean_spec
| c_boolean_spec ';' boolean_value
;
constraint_ref:
V_LOCAL_TERM_CODE_REF
;
any_identifier:
type_identifier
| V_ATTRIBUTE_IDENTIFIER
;
// for string_value etc, see dADL spec
// for attribute_path, object_path, call_path, etc, see Path spec
// for assertions, assertion, see Assertion spec5.5.2. Symbols
The following shows the lexical specification for the cADL grammar.
----------/* definitions */ -----------------------------------------------
ALPHANUM [a-zA-Z0-9]
IDCHAR [a-zA-Z0-9_]
NAMECHAR [a-zA-Z0-9._\-]
NAMECHAR_SPACE [a-zA-Z0-9._\- ]
NAMECHAR_PAREN [a-zA-Z0-9._\-()]
UTF8CHAR (([\xC2-\xDF][\x80-\xBF])|(\xE0[\xA0-\xBF][\x80-\xBF])|([\xE1-\xEF][\x80-\xBF][\x80-\xBF])|(\xF0[\x90-\xBF][\x80-\xBF][\x80-\xBF])|([\xF1-\xF7][\x80-\xBF][\x80-\xBF][\x80-\xBF]))
----------/* comments */ -------------------------------------------------
"--".* -- Ignore comments
"--".*\n[ \t\r]*
----------/* symbols */ -------------------------------------------------
"-" -- -> Minus_code
"+" -- -> Plus_code
"*" -- -> Star_code
"/" -- -> Slash_code
"^" -- -> Caret_code
"=" -- -> Equal_code
"." -- -> Dot_code
";" -- -> Semicolon_code
"," -- -> Comma_code
":" -- -> Colon_code
"!" -- -> Exclamation_code
"(" -- -> Left_parenthesis_code
")" -- -> Right_parenthesis_code
"$" -- -> Dollar_code
"??" -- -> SYM_DT_UNKNOWN
"?" -- -> Question_mark_code
"|" -- -> SYM_INTERVAL_DELIM
"[" -- -> Left_bracket_code
"]" -- -> Right_bracket_code
"{" -- -> SYM_START_CBLOCK
"}" -- -> SYM_END_CBLOCK
".." -- -> SYM_ELLIPSIS
"..." -- -> SYM_LIST_CONTINUE
----------/* common keywords */ --------------------------------------
[Mm][Aa][Tt][Cc][Hh][Ee][Ss] -- -> SYM_MATCHES
[Ii][Ss]_[Ii][Nn] -- -> SYM_MATCHES
----------/* assertion keywords */ ------------------------------------
[Tt][Hh][Ee][Nn] -- -> SYM_THEN
[Ee][Ll][Ss][Ee] -- -> SYM_ELSE
[Aa][Nn][Dd] -- -> SYM_AND
[Oo][Rr] -- -> SYM_OR
[Xx][Oo][Rr] -- -> SYM_XOR
[Nn][Oo][Tt] -- -> SYM_NOT
[Ii][Mm][Pp][Ll][Ii][Ee][Ss] -- -> SYM_IMPLIES
[Tt][Rr][Uu][Ee] -- -> SYM_TRUE
[Ff][Aa][Ll][Ss][Ee] -- -> SYM_FALSE
[Ff][Oo][Rr][_][Aa][Ll][Ll] -- -> SYM_FORALL
[Ee][Xx][Ii][Ss][Tt][Ss] -- -> SYM_EXISTS
---------/* cADL keywords */ ---------------------------------------
[Ee][Xx][Ii][Ss][Tt][Ee][Nn][Cc][Ee] -- -> SYM_EXISTENCE
[Oo][Cc][Cc][Uu][Rr][Rr][Ee][Nn][Cc][Ee][Ss] -- -> SYM_OCCURRENCES
[Cc][Aa][Rr][Dd][Ii][Nn][Aa][Ll][Ii][Tt][Yy] -- -> SYM_CARDINALITY
[Oo][Rr][Dd][Ee][Rr][Ee][Dd] -- -> SYM_ORDERED
[Uu][Nn][Oo][Rr][Dd][Ee][Rr][Ee][Dd] -- -> SYM_UNORDERED
[Uu][Nn][Ii][Qq][Uu][Ee] -- -> SYM_UNIQUE
[Ii][Nn][Ff][Ii][Nn][Ii][Tt][Yy] -- -> SYM_INFINITY
[Uu][Ss][Ee][_][Nn][Oo][Dd][Ee] -- -> SYM_USE_NODE
[Uu][Ss][Ee][_][Aa][Rr][Cc][Hh][Ee][Tt][Yy][Pp][Ee] -- -> SYM_USE_ARCHETYPE
[Aa][Ll][Ll][Oo][Ww][_][Aa][Rr][Cc][Hh][Ee][Tt][Yy][Pp][Ee] -- -> SYM_ALLOW_ARCHETYPE
[Ii][Nn][Cc][Ll][Uu][Dd][Ee] -- -> SYM_INCLUDE
[Ee][Xx][Cc][Ll][Uu][Dd][Ee] -- -> SYM_EXCLUDE
----------/* V_URI */ -----------------------------------------------
[a-z]+:\/\/[^<>|\\{}^~"\[\] ]*
---------/* V_QUALIFIED_TERM_CODE_REF */ ----------------------------
-- any qualified code, e.g. [local::at0001], [local::ac0001], [loinc::700-0]
--
\[{NAMECHAR_PAREN}+::{NAMECHAR}+\]
\[{NAMECHAR_PAREN}+::{NAMECHAR_SPACE}+\] -- error
---------/* V_LOCAL_TERM_CODE_REF */ ---------------------------------
-- any unqualified code, e.g. [at0001], [ac0001], [700-0]
--
\[{ALPHANUM}{NAMECHAR}*\]
----------/* V_LOCAL_CODE */ ----------------------------------------
a[ct][0-9.]+
---------/* V_TERM_CODE_CONSTRAINT of form */ ------------
-- [terminology_id::code, -- comment
-- code, -- comment
-- code] -- comment
--
-- Form with assumed value
-- [terminology_id::code, -- comment
-- code; -- comment
-- code] -- an optional assumed value
--
\[[a-zA-Z0-9()._\-]+::[ \t\n]* -- start IN_TERM_CONSTRAINT
<IN_TERM_CONSTRAINT> {
[ \t]*[a-zA-Z0-9._\-]+[ \t]*;[ \t\n]*
-- match second last line with ';' termination (assumed value)
[ \t]*[a-zA-Z0-9._\-]+[ \t]*,[ \t\n]*
-- match any line, with ',' termination
\-\-[^\n]*\n -- ignore comments
[ \t]*[a-zA-Z0-9._\-]*[ \t\n]*\] -- match final line, terminating in ']'
------/* V_ISO8601_EXTENDED_DATE_TIME */ ---
-- YYYY-MM-DDThh:mm:ss[,sss][Z|+/-nnnn]
--
[0-9]{4}-[0-1][0-9]-[0-3][0-9]T[0-2][0-9]:[0-6][0-9]:[0-6][0-9](,[0-9]+)?(Z|[+-][0-9]{4})? |
[0-9]{4}-[0-1][0-9]-[0-3][0-9]T[0-2][0-9]:[0-6][0-9](Z|[+-][0-9]{4})? |
[0-9]{4}-[0-1][0-9]-[0-3][0-9]T[0-2][0-9](Z|[+-][0-9]{4})?
----------/* V_ISO8601_EXTENDED_TIME */ --------
-- hh:mm:ss[,sss][Z|+/-nnnn]
--
[0-2][0-9]:[0-6][0-9]:[0-6][0-9](,[0-9]+)?(Z|[+-][0-9]{4})? |
[0-2][0-9]:[0-6][0-9](Z|[+-][0-9]{4})?
----------/* V_ISO8601_DATE YYYY-MM-DD */ --------------------
[0-9]{4}-[0-1][0-9]-[0-3][0-9] |
[0-9]{4}-[0-1][0-9]
----------/* V_ISO8601_DURATION */ -------------------------
P([0-9]+[yY])?([0-9]+[mM])?([0-9]+[wW])?([0-9]+[dD])?T([0-9]+[hH])?([0-9]+[mM])?([0-9]+[sS])? |
P([0-9]+[yY])?([0-9]+[mM])?([0-9]+[wW])?([0-9]+[dD])?
----------/* V_ISO8601_DATE_CONSTRAINT_PATTERN */ -----------------
[yY][yY][yY][yY]-[mM?X][mM?X]-[dD?X][dD?X]
----------/* V_ISO8601_TIME_CONSTRAINT_PATTERN */ ------------------
[hH][hH]:[mM?X][mM?X]:[sS?X][sS?X]
----------/* V_ISO8601_DATE_TIME_CONSTRAINT_PATTERN */ -------------
[yY][yY][yY][yY]-[mM?][mM?]-[dD?X][dD?X][ T][hH?X][hH?X]:[mM?X][mM?X]:[sS?X][sS?X]
----------/* V_ISO8601_DURATION_CONSTRAINT_PATTERN */ --------------
P[yY]?[mM]?[wW]?[dD]?T[hH]?[mM]?[sS]? |
P[yY]?[mM]?[wW]?[dD]?
----------/* V_TYPE_IDENTIFIER */ ------------------------------------
[A-Z]{IDCHAR}*
----------/* V_GENERIC_TYPE_IDENTIFIER */ ----------------------------
[A-Z]{IDCHAR}*<[a-zA-Z0-9,_<>]+>
----------/* V_FEATURE_CALL_IDENTIFIER */ ----------------------------
[a-z]{IDCHAR}*[ ]*\(\)
----------/* V_ATTRIBUTE_IDENTIFIER */ ----------------------------
[a-z]{IDCHAR}*
----------/* V_GENERIC_TYPE_IDENTIFIER */ -------------------------------
[A-Z]{IDCHAR}*<[a-zA-Z0-9,_<>]+>
----------/* V_ATTRIBUTE_IDENTIFIER */ ----------------------------------
[a-z]{IDCHAR}*
----------/* V_C_DOMAIN_TYPE - sections of dADL syntax */ ---------------
-- {mini-parser specification}
-- this is an attempt to match a dADL section inside cADL. It will
-- probably never work 100% properly since there can be '>' inside "||"
-- ranges, and also strings containing any character, e.g. units string
-- contining "{}" chars. The real solution is to use the dADL parser on
-- the buffer from the current point on and be able to fast-forward the
-- cursor to the last character matched by the dADL scanner
-- the following version matches a type name without () and is deprecated
[A-Z]{IDCHAR}*[ \n]*< -- match a pattern like
-- 'Type_Identifier whitespace <'
-- the following version is correct ADL 1.4/ADL 1.5
\([A-Z]{IDCHAR}*\)[ \n]*< -- match a pattern like
-- '(Type_Identifier) whitespace <'
<IN_C_DOMAIN_TYPE> {
[^}>]*>[ \n]*[^>}A-Z] -- match up to next > not
-- followed by a '}' or '>'
[^}>]*>+[ \n]*[}A-Z] -- final section - '...>
-- whitespace } or beginning of
-- a type identifier'
[^}>]*[ \n]*} -- match up to next '}' not
} -- preceded by a '>'
----------/* V_REGEXP */ -------------------------------------
-- {mini-parser specification}
"{/" -- start of regexp
<IN_REGEXP1>[^/]*\\\/ -- match any segments with quoted slashes
<IN_REGEXP1>[^/}]*\/ -- match final segment
\^[^^\n]*\^ -- regexp formed using '^' delimiters
----------/* V_INTEGER */ -----------------------------------------------
[0-9]+
----------/* V_REAL */ -----------------------------------------------
[0-9]+\.[0-9]+
[0-9]+\.[0-9]+[eE][+-]?[0-9]+
----------/* V_STRING */ -----------------------------------------------
\"[^\\\n"]*\"
\"[^\\\n"]*{ -- beginning of a multi-line string
<IN_STR> {
\\\\ -- match escaped backslash, i.e. \\ -> \
\\\" -- match escaped double quote, i.e. \" -> "
{UTF8CHAR}+ -- match UTF8 chars
[^\\\n"]+ -- match any other characters
\\\n[ \t\r]* -- match LF in line
[^\\\n"]*\" -- match final end of string
.|\n |
<<EOF>> -- unclosed String -> ERR_STRING
6. Assertions
6.1. Overview
This section describes the assertion sub-language of archetypes. Assertions are used in archetype "slot" clauses in the cADL definition section, and in the invariant section. The following simple assertion in an invariant clause says that the speed in kilometres of some node is related to the speed-in-miles by a factor of 1.6:
validity: /speed[at0002]/kilometres/magnitude = /speed[at0004]/miles/magnitude * 1.6The archetype assertion language is a small language of its own. Formally it is a first-order predicate logic with equality and comparison operators (=, >, etc). It is very nearly a subset of the OMG’s emerging OCL (Object Constraint Language) syntax, and is very similar to the assertion syntax which has been used in the [Object_Z] and [Eiffel] languages and tools for over a decade. (See [Sowa_2000], [Hein_2002], [Kilov_1994] for an explanation of predicate logic in information modelling.)
6.2. Keywords
The syntax of the invariant section is a subset of first-order predicate logic. In it, the following keywords can be used:
-
exists,for_all, -
and,or,xor,not,implies -
true,false
Symbol equivalents for some of the above are given in the following table.
| Textual Rendering |
Symbolic Rendering |
Meaning |
|---|---|---|
matches, is_in |
∈ |
Set membership, "p is in P" |
exists |
∃ |
Existential quantifier, "there exists …" |
for_all |
∀ |
Universal quantifier, "for all x…" |
implies |
® |
Material implication, "p implies q", or "if p then q" |
and |
∧ |
Logical conjunction, "p and q" |
or |
∨ |
Logical disjunction, "p or q" |
xor |
∨ |
Exclusive or, "only one of p or q" |
not, ~ |
∼, ¬ |
Negation, "not p" |
The not operator can be applied as a prefix operator to all other operators except for_all; either textual rendering not or ~ can be used.
6.3. Operators
Assertion expressions can include arithmetic, relational and boolean operators, plus the existential and universal quantifiers.
6.3.1. Arithmetic Operators
The supported arithmetic operators are as follows:
-
addition:
+ -
subtraction:
- -
multiplication:
* -
division:
/ -
exponent:
^ -
modulo division:
%— remainder after integer division
6.3.2. Equality Operators
The supported equality operators are as follows:
-
equality:
= -
inequality:
<>
The semantics of these operators are of value comparison.
6.3.3. Relational Operators
The supported relational operators are as follows:
-
less than:
< -
less than or equal:
<= -
greater than:
> -
greater than or equal:
>=
The semantics of these operators are of value comparison on entities of Comparable types (see openEHR Support IM, Assumed Types section). All generate a Boolean result.
6.4. Operands
Operands in an assertion expression can be any of the following:
- manifest constant
-
any constant of any primitive type, expressed according to the dADL syntax for values;
- variable reference
-
any name starting with
$, e.g.$body_weight; - object reference
-
a path referring to an object node, i.e. any path ending in a node identifier;
- property reference
-
a path referring to a property, i.e. any path ending in
.property_name.
If an assertion is used in an archetype slot definition, its paths refer to the archetype filling the slot, not the one containing the slot.
6.6. Future
6.6.1. Variables
TBD: : main problem of variables is that they must have names, which are language-dependent; imagine if there were a mixture of variables added by authors in different languages. The only solution is to name them with terms.
TBD: : Variables have to be treated as term coordinations, and should be coded e.g. using ccNNNN codes (“cc” = coordinated code). Then they can be given meanings in any language.
6.6.1.1. Predefined Variables
A number of predefined variables can be referenced in ADL assertion expressions, without prior definition, including:
-
$current_date: Date; returns the date whenever the archetype is evaluated -
$current_time: Time; returns time whenever the archetype is evaluated -
$current_date_time: Date_Time; returns date/time whenever the archetype is evaluated
To Be Continued: these should be coded as well, using openEHR codes
6.6.1.2. Archetype-defined Variables
Variables can also be defined inside an archetype, as part of the assertion statements in an invariant. The syntax of variable definition is as follows:
let $var_name = reference
Here, a reference can be any of the operand types listed above. 'Let' statements can come anywhere in an invariant block, but for readability, should generally come first.
The following example illustrates the use of variables in an invariant block:
invariant
let $sys_bp = /data[at9001]/events[at9002]/data[at1000]/items[at1100]
let $dia_bp = /data[at9001]/events[at9002]/data[at1000]/items[at1200]
$sys_bp >= $dia_bp
6.7. Syntax Specification
The assertion grammar is part of the cADL grammar. This grammar is implemented and tested using lex (.l file) and yacc (.y file) specifications for in the Eiffel programming environment. The 1.4 release of these files is available in the cADL grammar files. The .l and .y files can be converted for use in another yacc/lex-based programming environment.
6.7.1. Grammar
The following provides the assertion parser production rules (yacc specification). Note that because of interdependencies with path and assertion production rules, practical implementations may have to include all production rules in one parser.
assertions:
assertion
| assertions assertion
;
assertion:
any_identifier ':' boolean_expression
| boolean_expression
;
boolean_expression:
boolean_leaf
| boolean_node
;
boolean_node:
SYM_EXISTS absolute_path
| relative_path SYM_MATCHES SYM_START_CBLOCK c_primitive SYM_END_CBLOCK
| SYM_NOT boolean_leaf
| arithmetic_expression '=' arithmetic_expression
| arithmetic_expression SYM_NE arithmetic_expression
| arithmetic_expression SYM_LT arithmetic_expression
| arithmetic_expression SYM_GT arithmetic_expression
| arithmetic_expression SYM_LE arithmetic_expression
| arithmetic_expression SYM_GE arithmetic_expression
| boolean_expression SYM_AND boolean_expression
| boolean_expression SYM_OR boolean_expression
| boolean_expression SYM_XOR boolean_expression
| boolean_expression SYM_IMPLIES boolean_expression
;
boolean_leaf:
'(' boolean_expression ')'
| SYM_TRUE
| SYM_FALSE
;
arithmetic_expression:
arithmetic_leaf
| arithmetic_node
;
arithmetic_node:
arithmetic_expression '+' arithmetic_leaf
| arithmetic_expression '-' arithmetic_leaf
| arithmetic_expression '*' arithmetic_leaf
| arithmetic_expression '/' arithmetic_leaf
| arithmetic_expression '^' arithmetic_leaf
;
arithmetic_leaf:
'(' arithmetic_expression ')'
| integer_value
| real_value
| absolute_path
;7. ADL Paths
7.1. Overview
The notion of paths is integral to ADL, and a common path syntax is used to reference nodes in both dADL and cADL sections of an archetype. The same path syntax works for both, because both dADL and cADL have an alternating object/attribute structure. However, the interpretation of path expressions in dADL and cADL differs slightly; the differences are explained in the dADL and cADL sections of this document. This section describes only the common syntax and semantics.
The general form of the path syntax is as follows (see syntax section below for full specification):
path: '/'? path_segment ( '/' path_segment )+ ;
path_segment: attr_name ( '[' object_id ']' )? ;Essentially, ADL paths consist of segments separated by slashes ('/'), where each segment is an attribute name with optional object identifier predicate, indicated by brackets ('[]').
ADL Paths are formed from an alternation of segments made up of an attribute name and optional object node identifier predicate, separated by slash ('/') characters. Node identifiers are delimited by brackets (i.e. []).
Similarly to paths used in file systems, ADL paths are either absolute or relative, with the former being indicated by a leading slash.
Paths are absolute or relative with respect to the document in which they are mentioned. Absolute paths commence with an initial slash ('/') character.
The ADL path syntax also supports the concept of "movable" path patterns, i.e. paths that can be used to find a section anywhere in a hierarchy that matches the path pattern. Path patterns are indicated with a leading double slash ('//') as in Xpath.
Path patterns are absolute or relative with respect to the document in which they are mentioned. Absolute paths commence with an initial slash ('/') character.
7.2. Relationship with W3C Xpath
The ADL path syntax is semantically a subset of the Xpath query language, with a few syntactic shortcuts to reduce the verbosity of the most common cases. Xpath differentiates between "children" and "attributes" sub-items of an object due to the difference in XML between Elements (true sub-objects) and Attributes (tag-embedded primitive values). In ADL, as with any pure object formalism, there is no such distinction, and all subparts of any object are referenced in the manner of Xpath children; in particular, in the Xpath abbreviated syntax, the key child:: does not need to be used.
ADL does not distinguish attributes from children, and also assumes the node_id attribute. Thus, the following expressions are legal for cADL structures:
items[1] -- the first member of 'items'
items[systolic] -- the member of 'items' with meaning 'systolic'
items[at0001] -- the member of 'items' with node id 'at0001'The Xpath equivalents are:
items[1] -- the first member of 'items'
items[meaning() = 'systolic'] -- the member of 'items' for which the meaning()
-- function evaluates to "systolic"
items[@archetype_node_id = 'at0001'] -- the member of 'items' with key 'at0001'In the above, meaning() is a notional function is defined for Xpath in openEHR, which returns the rubric for the node_id of the current node. Such paths are only for display purposes, and paths used for computing always use the 'at' codes, e.g. items[at0001], for which the Xpath equivalent is items[@node_id = 'at0001'].
The ADL movable path pattern is a direct analogue of the Xpath syntax abbreviation for the 'descendant' axis.
7.3. Syntax Specification
The path grammar is part of the cADL grammar. This grammar is implemented and tested using lex (.l file) and yacc (.y file) specifications for in the Eiffel programming environment. The 1.4 release of these files is available in the cADL grammar files. The .l and .y files can be converted for use in another yacc/lex-based programming environment.
7.3.1. Grammar
The following provides the assertion parser production rules (yacc specification). Note that because of interdependcies with path and assertion production rules, practical implementations may have to include all production rules in one parser.
input:
movable_path
| absolute_path
| relative_path
;
movable_path:
SYM_MOVABLE_LEADER relative_path
absolute_path:
'/' relative_path
| absolute_path '/' relative_path
;
relative_path:
path_segment
| relative_path '/' path_segment
;
path_segment:
V_ATTRIBUTE_IDENTIFIER V_LOCAL_TERM_CODE_REF
| V_ATTRIBUTE_IDENTIFIER
;7.3.2. Symbols
The following specifies the symbols and lexical patterns used in the path grammar.
----------/* symbols */ ------------------------------------------------- "." -- -> Dot_code "/" -- -> Slash_code "[" -- -> Left_bracket_code "]" -- -> Right_bracket_code "//" -- -> SYM_MOVABLE_LEADER ----------/* term code reference */ ------------------------------------- \[[a-zA-Z0-9][a-zA-Z0-9._\-]*\] -- -> V_LOCAL_TERM_CODE_REF ----------/* identifiers */ --------------------------------------------- [a-z][a-zA-Z0-9_]* -- -> V_ATTRIBUTE_IDENTIFIER
8. ADL - Archetype Definition Language
8.1. Introduction
This section describes ADL archetypes as a whole, adding a small amount of detail to the descriptions of dADL and cADL already given. The important topic of the relationship of the cADL-encoded definition section and the dADL-encoded ontology section is discussed in detail. In this section, only standard ADL (i.e. the cADL and dADL constructs and types described so far) is assumed. Archetypes for use in particular domains can also be built with more efficient syntax and domain-specific types, as described in Section 9, and the succeeding sections.
An ADL archetype follows the structure shown below:
archetype
archetype_id
[specialize
parent_archetype_id]
concept
coded_concept_name
language
dADL language description section
[description
dADL meta-data description section]
definition
cADL structural section
invariant
assertions
ontology
dADL definitions section
[revision_history
dADL section]
8.2. Basics
8.2.1. Keywords
ADL has a small number of keywords which are reserved for use in archetype declarations, as follows:
-
archetype,specialise/specialize,concept, -
language, -
description,definition,invariant,ontology
All of these words can safely appear as identifiers in the definition and ontology sections.
8.2.2. Node Identification
In the definition section of an ADL archetype, a particular scheme of codes is used for node identifiers as well as for denoting constraints on textual (i.e. language dependent) items. Codes are either local to the archetype, or from an external lexicon. This means that the archetype description is the same in all languages, and is available in any language that the codes have been translated to. All term codes are shown in brackets ([]). Codes used as node identifiers and defined within the same archetype are prefixed with at and by convention have 4 digits, e.g. [at0010]. Codes of any length are acceptable in ADL archetypes. Specialisations of locally coded concepts have the same root, followed by 'dot' extensions, e.g. [at0010.2]. From a terminology point of view, these codes have no implied semantics - the 'dot' structuring is used as an optimisation on node identification.
8.2.3. Local Constraint Codes
A second kind of local code is used to stand for constraints on textual items in the body of the archetype. Although these could be included in the main archetype body, because they are language- and/or terminology-sensitive, they are defined in the ontology section, and referenced by codes prefixed by ac, e.g. [ac0009]. As for at codes, the convention used in this document is to use 4-digit ac codes, even though any number of digits is acceptable. The use of these codes is described in section
[Constraint_definitions section].
8.3. Header Sections
8.3.1. Archetype Section
This section introduces the archetype and must include an identifier. A typical archetype section is as follows:
archetype (adl_version=1.4)
openEHR-EHR-OBSERVATION.haematology.v1The multi-axial identifier identifies archetypes in a global space. The syntax of the identifier is described in [Archetype Identification] in The openEHR Archetype System.
8.3.2. Controlled Indicator
A flag indicating whether the archetype is change-controlled or not can be included after the version, as follows:
archetype (adl_version=1.4; controlled)
openEHR-EHR-OBSERVATION.haematology.v1This flag may have the two values "controlled" and "uncontrolled" only, and is an aid to software. Archetypes that include the "controlled" flag should have the revision history section included, while those with the "uncontrolled" flag, or no flag at all, may omit the revision history. This enables archetypes to be privately edited in an early development phase without generating large revision histories of little or no value.
8.3.3. Specialise Section
This optional section indicates that the archetype is a specialisation of some other archetype, whose identity must be given. Only one specialisation parent is allowed, i.e. an archetype cannot 'multiply-inherit' from other archetypes. An example of declaring specialisation is as follows:
archetype (adl_version=1.4)
openEHR-EHR-OBSERVATION.haematology-cbc.v1
specialise
openEHR-EHR-OBSERVATION.haematology.v1Here the identifier of the new archetype is derived from that of the parent by adding a new section to its domain concept section. See the ARCHETYPE_ID definition in the identification package in the openEHR Support IM specification.
|
Note
|
both the US and British English versions of the word "specialise" are valid in ADL. |
8.3.4. Concept Section
All archetypes represent some real world concept, such as a "patient", a "blood pressure", or an "antenatal examination". The concept is always coded, ensuring that it can be displayed in any language the archetype has been translated to. A typical concept section is as follows:
concept
[at0010] -- haematology result
In this concept definition, the term definition of [at0010] is the proper description corresponding to the "haematology-cbc" section of the archetype id above.
8.3.5. Language Section and Language Translation
The language section includes data describing the original language in which the archetype was authored (essential for evaluating natural language quality), and the total list of languages available in the archetype. There can be only one original_language. The translations list must be updated every time a translation of the archetype is undertaken. The following shows a typical example.
language
original_language = <[iso_639-1::en]>
translations = <
["de"] = <
language = <[iso_639-1::de]>
author = <
["name"] = <"Frederik Tyler">
["email"] = <"freddy@something.somewhere.co.uk">
>
accreditation = <"British Medical Translator id 00400595">
>
["ru"] = <
language = <[iso_639-1::ru]>
author = <
["name"] = <"Nina Alexandrovna">
["organisation"] = <"Dostoevsky Media Services">
["email"] = <"nina@translation.dms.ru">
>
accreditation = <"Russian Translator id 892230-3A">
>
>Archetypes must always be translated completely, or not at all, to be valid. This means that when a new translation is made, every language dependent section of the description and ontology sections has to be translated into the new language, and an appropriate addition made to the translations list in the language section.
|
Note
|
some non-conforming ADL tools in the past created archetypes without a language section, relying on the ontology section to provide the original_language (there called primary_language) and list of languages (languages_available). In the interests of backward compatibility, tool builders should consider accepting archetypes of the old form and upgrading them when parsing to the correct form, which should then be used for serialising/saving.
|
8.3.6. Description Section
The description section of an archetype contains descriptive information, or what some people think of as document "meta-data", i.e. items that can be used in repository indexes and for searching. The dADL syntax, described in Section 4, is used for the description, as in the following example.
description
original_author = <
["name"] = <"Dr J Joyce">
["organisation"] = <"NT Health Service">
["date"] = <2003-08-03>
>
lifecycle_state = <"initial">
resource_package_uri = <"http://www.aihw.org.au/data_sets/diabetic_archetypes.html">
details = <
["en"] = <
language = <[iso_639-1::en]>
purpose = <"archetype for diabetic patient review">
use = <"used for all hospital or clinic-based diabetic reviews,
including first time. Optional sections are removed according to the particular review">
misuse = <"not appropriate for pre-diagnosis use">
original_resource_uri = <"http://www.healthdata.org.au/data_sets/diabetic_review_data_set_1.html">
other_details = <...>
>
["de"] = <
language = <[iso_639-1::de]>
purpose = <"Archetyp für die Untersuchung von Patienten mit Diabetes">
use = <"wird benutzt für alle Diabetes-Untersuchungen im
Krankenhaus, inklusive der ersten Vorstellung. Optionale
Abschnitte werden in Abhängigkeit von der speziellen
Vorstellung entfernt.">
misuse = <"nicht geeignet für Benutzung vor Diagnosestellung">
original_resource_uri = <"http://www.healthdata.org.au/data_sets/diabetic_review_data_set_1.html">
other_details = <...>
>
>
other_details = <...>A number of details are worth noting here. Firstly, the free hierarchical structuring capability of dADL is exploited for expressing the 'deep' structure of the details section and its subsections. Secondly, the dADL qualified list form is used to allow multiple translations of the purpose and use to be shown. Lastly, empty items such as misuse (structured if there is data) are shown with just one level of empty brackets. The above example shows meta-data based on the openEHR Archetype Object Model (AOM).
The description section is technically optional according to the AOM, but in any realistic use of ADL for archetypes, it will be required. A minimal description section satisfying to the AOM is as follows:
description
original_author = <
["name"] = <"Dr J Joyce">
["organisation"] = <"NT Health Service">
["date"] = <2003-08-03>
>
lifecycle_state = <"initial">
details = <
["en"] = <
language = <[iso_639-1::en]>
purpose = <"archetype for diabetic patient review">
>
>8.3.6.1. Extending meta-data
The description section models a specific set of meta-data items, but of course, the meta-data needs over time can never be fully predicted. To enable free extension of the description section, the other_details is used. Its structure takes the form of a Hash of strings, i.e. Hash <String, String>, and can be used to contain other meta-data items not explicitly modelled.
The Appendix B Appendix describes the known uses of extended meta-data to date.
8.4. Definition Section
The definition section contains the main formal definition of the archetype, and is written in the Constraint Definition Language). A typical definition section is as follows:
definition
OBSERVATION[at0000] ∈ { -- blood pressure measurement
name ∈ { -- any synonym of BP
CODED_TEXT ∈ {
defining_code ∈ {
CODE_PHRASE ∈ {[ac0001]}
}
}
}
data ∈ {
HISTORY[at9001] ∈ { -- history
events cardinality ∈ {1..*} ∈ {
EVENT[at9002] occurrences ∈ {0..1} ∈ { -- baseline
name ∈ {
CODED_TEXT ∈ {
defining_code ∈ {
CODE_PHRASE ∈ {[ac0002]}
}
}
}
data ∈ {
ITEM_LIST[at1000] ∈ { -- systemic arterial BP
items cardinality ∈ {2..*} ∈ {
ELEMENT[at1100] ∈ { -- systolic BP
name ∈ { -- any synonym of 'systolic'
CODED_TEXT ∈ {
defining_code ∈ {
CODE_PHRASE ∈ {[ac0002]}
}
}
}
value ∈ {
QUANTITY ∈ {
magnitude ∈ {|0..1000|}
property ∈ {[properties::944]} -- "pressure"
units ∈ {[units::387]} -- "mm[Hg]"
}
}
}
ELEMENT[at1200] ∈ { -- diastolic BP
name ∈ { -- any synonym of 'diastolic'
CODED_TEXT ∈ {
defining_code ∈ {
CODE_PHRASE ∈ {[ac0003]}
}
}
}
value ∈ {
QUANTITY ∈ {
magnitude ∈ {|0..1000|}
property ∈ {[properties::944]} -- "pressure"
units ∈ {[units::387]} -- "mm[Hg]"
}
}
}
ELEMENT[at9000] occurrences ∈ {0..*} ∈ {*} -- unknown new item
}
...This definition expresses constraints on instances of the types ENTRY , HISTORY , EVENT , ITEM_LIST , ELEMENT , QUANTITY , and CODED_TEXT so as to allow them to represent a blood pressure measurement, consisting of a history of measurement events, each consisting of at least systolic and diastolic pressures, as well as any number of other items (expressed by the [at9000] "any" node near the bottom).
8.4.1. Design-time and Run-time paths
All non-unique sibling nodes in a cADL text that correspond to nodes in data which might be referred to from elsewhere in the archetype (via use_node), or might be queryied at runtime, require a node identifier. It is preferable to assign a 'design-time meaning', enabling paths and queries to be expressed using logical meanings rather than meaningless identifiers. When data are created according to the definition section of an archetype, the archetype node identifiers can be written into the data, providing a reliable way of finding data nodes, regardless of what other runtime names might have been chosen by the user for the node in question. There are two reasons for doing this. Firstly, querying cannot rely on runtime names of nodes (e.g. names like "sys BP", "systolic bp", "sys blood press." entered by a doctor are unreliable for querying); secondly, it allows runtime data retrieved from a persistence mechanism to be re-associated with the cADL structure which was used to create it.
An example which shows the difference between design-time meanings associated with node identifiers and runtime names is the following, from a SECTION archetype representing the problem/SOAP headings (a simple heading structure commonly used by clinicians to record patient contacts under top-level headings corresponding to the patient’s problem(s), and under each problem heading, the headings "subjective", "objective", "assessment", and "plan").
SECTION[at0000] matches { -- problem
name matches {
CODED_TEXT matches {
defining_code matches {[ac0001]} -- any clinical problem type
}
}
}In the above, the node identifier [at0000] is assigned a meaning such as "clinical problem" in the archetype terminology section. The subsequent lines express a constraint on the runtime name attribute, using the internal code [ac0001] . The constraint [ac0001] is also defined in the archetype terminology section with a formal statement meaning "any clinical problem type", which could clearly evaluate to thousands of possible values, such as "diabetes", "arthritis" and so on. As a result, in the runtime data, the node identifier corresponding to "clinical problem" and the actual problem type chosen at runtime by a user, e.g. "diabetes", can both be found. This enables querying to find all nodes with meaning "problem", or all nodes describing the problem "diabetes". Internal [acNNNN] codes are described in Section 8.2.3.
8.5. Invariant Section
The rules section in an ADL archetype introduces assertions which relate to the entire archetype, and can be used to make statements which are not possible within the block structure of the definition section. Any constraint which relates more than one property to another is in this category, as are most constraints containing mathematical or logical formulae. Rules are expressed in the archetype assertion language, described in Section 6.
An assertion is a first order predicate logic statement which can be evaluated to a boolean result at runtime. Objects and properties are referred to using paths.
The following simple example says that the speed in kilometres of some node is related to the speed-in-miles by a factor of 1.6:
invariant
validity: /speed[at0002]/kilometres/magnitude = /speed[at0004]/miles/magnitude * 1.68.6. Ontology Section
8.6.1. Overview
The ontology section of an archetype is expressed in dADL, and is where codes representing node identifiers, constraints on coded term values, and bindings to terminologies are defined. Linguistic language translations are added in the form of extra blocks keyed by the relevant language. The following example shows the general layout of this section.
ontology
terminologies_available = <"snomed_ct", ...>
term_definitions = <
["en"] = <
items = <...>
>
["de"] = <
items = <...>
>
>
constraint_definitions = <
["en"] = <
items = <...>
>
["de"] = <
items = <...>
>
>
term_bindings = <
["snomed_ct"] = <
items = <...>
...
>
>
constraint_bindings = <
["snomed_ct"] = <
items = <...>
...
>
>The term_definitions section is mandatory, and must be defined for each translation carried out. Each of these sections can have its own meta-data, which appears within description sub-sections, such as the one shown above providing translation details.
8.6.2. Ontology Header Statements
The terminologies_available statement includes the identifiers of all terminologies for which term_bindings sections have been written.
|
Note
|
some ADL tools in the past created archetypes with primary_language and languages_available statements rather than the original_languages and translations blocks in the language section. In the interests of backward compatibility, tool builders should consider accepting archetypes of the old form and upgrading them when parsing to the correct form, which should then be used for serialising/saving.
|
8.6.3. Term_definitions Section
This section is where all archetype local terms (that is, terms of the form [atNNNN]) are defined. The following example shows an extract from the English and German term definitions for the archetype local terms in a problem/SOAP headings archetype. Each term is defined using a structure of name/value pairs, and mustat least include the names "text" and "description", which are akin to the usual rubric, and full definition found in terminologies like SNOMED-CT. Each term object is then included in the appropriate language list of term definitions, as shown in the example below.
term_definitions = <
["en"] = <
items = <
["at0000"] = <
text = <"problem">
description = <"The problem experienced by the subject of care to which the contained information relates">
>
["at0001"] = <
text = <"problem/SOAP headings">
description = <"SOAP heading structure for multiple problems">
>
...
["at4000"] = <
text = <"plan">
description = <"The clinician's professional advice">
>
>
>
["de"] = <
items = <
["at0000"] = <
text = <"klinisches Problem">
description = <"Das Problem des Patienten worauf sich diese Informationen beziehen">
>
["at0001"] = <
text = <"Problem/SOAP Schema">
description = <"SOAP-Schlagwort-Gruppierungsschema fuer mehrfache Probleme">
>
["at4000"] = <
text = <"Plan">
description = <"Klinisch-professionelle Beratung des Pflegenden">
>
>
>
>In some cases, term definitions may have been lifted from existing terminologies (only a safe thing to do if the definitions exactly match the need in the archetype). To indicate where definitions come from, a "provenance" tag can be used, as follows:
["at4000"] = <
text = <"plan">
description = <"The clinician's professional advice">
provenance = <"ACME_terminology(v3.9a)">
>Note that this does not indicate a binding to any term, only the origin of its definition. Bindings are described below.
|
Note
|
the use of items in the above is historical in ADL, and will be changed in ADL2 to the proper form of dADl for nested containers, i.e. removing the "items = <" blocks altogether.
|
8.6.4. Constraint_definitions Section
The constraint_definitions section is of exactly the same form as the term_definitions section, and provides the definitions - i.e. the meanings - of the local constraint codes, which are of the form [acNNNN]. Each such code refers to some constraint such as "any term which is a subtype of 'hepatitis' in the ICD10AM terminology"; the constraint definitions do not provide the constraints themselves, but define the meanings of such constraints, in a manner comprehensible to human beings, and usable in GUI applications. This may seem a superfluous thing to do, but in fact it is quite important. Firstly, term constraints can only be expressed with respect to particular terminologies - a constraint for "kind of hepatitis" would be expressed in different ways for each terminology which the archetype is bound to. For this reason, the actual constraints are defined in the constraint_bindings section. An example of a constraint term definition for the hepatitis constraint is as follows:
items = <
["ac1015"] = <
text = <"type of hepatitis">
description = <"any term which means a kind of viral hepatitis">
>
>Note that while it often seems tempting to use classification codes, e.g. from the ICD vocabularies, these will rarely be much use in terminology or constraint definitions, because it is nearly always descriptive, not classificatory terms which are needed.
8.6.5. Term_bindings Section
This section is used to describe the equivalences between archetype local terms and terms found in external terminologies. The main purpose for allowing query engine software that wants to search for an instance of some external term to determine what equivalent to use in the archetype. Note that this is distinct from the process of embedding mapped terms in runtime data, which is also possible with the openEHR Reference Model DV_TEXT and DV_CODED_TEXT types.
8.6.5.1. Global Term Bindings
There are two types of term bindings that can be used, 'global' and path-based. The former is where an external term is bound directly to an archetype local term, and the binding holds globally throughout the archetype. In many cases, archetype terms only appear once in an archetype, but in some archetypes, at-codes are reused throughout the archetype. In such cases, a global binding asserts that the correspondence is true in all locations. A typical global term binding section resembles the following:
term_bindings = <
["umls"] = <
items =<
["at0000"] = <[umls::C124305]> -- apgar result
["at0002"] = <[umls::0000000]> -- 1-minute event
["at0004"] = <[umls::C234305]> -- cardiac score
["at0005"] = <[umls::C232405]> -- respiratory score
["at0006"] = <[umls::C254305]> -- muscle tone score
["at0007"] = <[umls::C987305]> -- reflex response score
["at0008"] = <[umls::C189305]> -- color score
["at0009"] = <[umls::C187305]> -- apgar score
["at0010"] = <[umls::C325305]> -- 2-minute apgar
["at0011"] = <[umls::C725354]> -- 5-minute apgar
["at0012"] = <[umls::C224305]> -- 10-minute apgar
>
>
>Each entry indicates which term in an external terminology is equivalent to the archetype internal codes. Note that not all internal codes necessarily have equivalents: for this reason, a terminology binding is assumed to be valid even if it does not contain all of the internal codes.
8.6.5.2. Path-based Bindings
The second kind of binding is one between an archetype path and an external code. This occurs commonly for archetypes where a term us re-used at the leaf level. For example, in the binding example below, the at0004 code represents 'temperature' and the codes at0003, at0005, at0006 etc correspond to various times such as 'any', 1-hour average, 1-hour maximum and so on. Some terminologies (notably LOINC, the laboratory terminology in this example) define 'pre-coordinated' codes, such as '1 hour body temperature'; these clearly correspond not to single codes such as at0004 in the archetype, but to whole paths. In such cases, the key in each term binding row is a full path rather than a single term.
["LNC205"] = <
items = <
["/data[at0002]/events[at0003]/data[at0001]/item[at0004]"] = <[LNC205::8310-5]>
["/data[at0002]/events[at0005]/data[at0001]/item[at0004]"] = <[LNC205::8321-2]>
["/data[at0002]/events[at0006]/data[at0001]/item[at0004]"] = <[LNC205::8311-3]>
["/data[at0002]/events[at0007]/data[at0001]/item[at0004]"] = <[LNC205::8316-2]>
["/data[at0002]/events[at0008]/data[at0001]/item[at0004]"] = <[LNC205::8332-0]>
["/data[at0002]/events[at0009]/data[at0001]/item[at0004]"] = <[LNC205::8312-1]>
["/data[at0002]/events[at0017]/data[at0001]/item[at0004]"] = <[LNC205::8325-3]>
["/data[at0002]/events[at0019]/data[at0001]/item[at0004]"] = <[LNC205::8320-4]>
>
>8.6.6. Constraint_bindings Section
The last of the ontology sections formally describes bindings to placeholder constraints (see Section 5.3.9) from the main archetype body. They are described separately because they are terminology-dependent, and because there may be more than one for a given logical constraint. A typical example follows:
constraint_bindings = <
["snomed_ct"] = <
items = <
["ac0001"] = <http://terminology.org?query_id=12345>
["ac0002"] = <http://terminology.org?query_id=678910>
>
>
>In this example, each local constraint code is formally defined to refer to a query defined in a terminology service, in this case, a terminology service that can interrogate the Snomed-CT terminology.
8.7. Revision History Section
The revision history section of an archetype shows the audit history of changes to the archetype, and is expressed in dADL syntax. It is optional, and is included at the end of the archetype, since it does not contain content of direct interest to archetype authors, and will monotonically grow in size. Where archetypes are stored in a version-controlled repository such as CVS or some commercial product, the revision history section would normally be regenerated each time by the authoring software, e.g. via processing of the output of the 'prs' command used with SCCS files, or 'rlog' for RCS files. The following shows a typical example, with entries in most-recent-first order (although technically speaking, the order is irrelevant to ADL).
revision_history
revision_history = <
["1.57"] = <
committer = <"Miriam Hanoosh">
committer_organisation = <"AIHW.org.au">
time_committed = <2004-11-02 09:31:04+1000>
revision = <"1.2">
reason = <"Added social history section">
change_type = <"Modification">
>
-- etc
["1.1"] = <
committer = <"Enrico Barrios">
committer_organisation = <"AIHW.org.au">
time_committed = <2004-09-24 11:57:00+1000>
revision = <"1.1">
reason = <"Updated HbA1C test result reference">
change_type = <"Modification">
>
["1.0"] = <
committer = <"Enrico Barrios">
committer_organisation = <"AIHW.org.au">
time_committed = <2004-09-14 16:05:00+1000>
revision = <"1.0">
reason = <"Initial Writing">
change_type = <"Creation">
>
>8.8. Validity Rules
This section describes the formal (i.e. checkable) semantics of ADL archetypes. It is recommended that parsing tools use the identifiers published here in their error messages, as an aid to archetype designers.
8.8.1. Global Archetype Validity
The following validity constraints apply to an archetype as a whole. Note that the term "section" means the same as "attribute" in the following, i.e. a section called "definition" in a dADL text is a serialisation of the value for the attribute of the same name.
VARID: archetype identifier validity. The archetype must have an identifier value for the archetype_id section. The identifier must conform to the published openEHR specification for archetype identifiers.
VARCN: archetype concept validity. The archetype must have an archetype term value in the concept section. The term must exist in the archetype ontology.
VARDF: archetype definition validity. The archetype must have a definition section, expressed as a cADL syntax string, or in an equivalent plug-in syntax.
VARON: archetype ontology validity. The archetype must have an ontology section, expressed as a cADL syntax string, or in an equivalent plug-in syntax.
VARDT: archetype definition typename validity. The topmost typename mentioned in the archetype definition section must match the type mentioned in the type-name slot of the first segment of the archetype id.
8.8.2. Coded Term Validity
All node identifiers ('at' codes) used in the definition part of the archetype must be defined in the term_definitions part of the ontology.
VATDF: archetype term validity. Each archetype term used as a node identifier the archetype definition must be defined in the term_definitions part of the ontology. All constraint identifiers ('ac' codes) used in the definition part of the archetype must be defined in the constraint_definitions part of the ontology.
VACDF: node identifier validity. Each constraint code used in the archetype definition part must be defined in the constraint_definitions part of the ontology.
8.8.3. Definition Section
The following constraints apply to the definition section of the archetype.
VDFAI: archetype identifier validity in definition. Any archetype identifier mentioned in an archetype slot in the definition section must conform to the published openEHR specification for archetype identifiers.
VDFPT: path validity in definition. Any path mentioned in the definition section must be valid syntactically, and a valid path with respect to the hierarchical structure of the definition section.
8.9. Syntax Specification
The following syntax and lexical specification are used to process an entire ADL file. Their main job is reading the header items, and then cutting it up into dADL, cADL and assertion sections.
The ADL grammar is implemented and tested using lex (.l file) and yacc (.y file) specifications for in the Eiffel programming environment. The 1.4 release of these files is available in the ADL grammar files. The .l and .y files can be converted for use in another yacc/lex-based programming environment.
8.9.1. Grammar
This section describes the ADL grammar.
archetype:
arch_identification
arch_specialisation
arch_concept
arch_language
arch_description
arch_definition
arch_invariant
arch_ontology
;
arch_identification:
arch_head V_ARCHETYPE_ID
;
arch_head:
SYM_ARCHETYPE
| SYM_ARCHETYPE arch_meta_data
;
arch_meta_data:
'(' arch_meta_data_items ')'
;
arch_meta_data_items:
arch_meta_data_item
| arch_meta_data_items ';' arch_meta_data_item
;
arch_meta_data_item:
SYM_ADL_VERSION '=' V_VERSION_STRING
| SYM_IS_CONTROLLED
;
arch_specialisation:
// empty OK
| SYM_SPECIALIZE V_ARCHETYPE_ID
;
arch_concept:
SYM_CONCEPT V_LOCAL_TERM_CODE_REF
| SYM_CONCEPT error
;
arch_language:
// empty OK
| SYM_LANGUAGE V_DADL_TEXT
;
arch_description:
// empty OK
| SYM_DESCRIPTION V_DADL_TEXT
;
arch_definition:
SYM_DEFINITION V_CADL_TEXT
;
arch_invariant:
// empty OK
| SYM_INVARIANT V_ASSERTION_TEXT
arch_ontology:
SYM_ONTOLOGY V_DADL_TEXT
;8.9.2. Symbols
The following shows the ADL lexical specification.
----------/* symbols */ -------------------------------------------------
"-" Minus_code
"+" Plus_code
"*" Star_code
"/" Slash_code
"^" Caret_code
"=" Equal_code
"." Dot_code
";" Semicolon_code
"," Comma_code
":" Colon_code
"!" Exclamation_code
"(" Left_parenthesis_code
")" Right_parenthesis_code
"$" Dollar_code
"?" Question_mark_code
"[" Left_bracket_code
"]" Right_bracket_code
----------/* keywords */ -------------------------------------------------
^[Aa][Rr][Cc][Hh][Ee][Tt][Yy][Pp][Ee][ \t\r]*\n SYM_ARCHETYPE
^[Ss][Pp][Ee][Cc][Ii][Aa][Ll][Ii][SsZz][Ee][ \t\r]*\n SYM_SPECIALIZE
^[Cc][Oo][Nn][Cc][Ee][Pp][Tt][ \t\r]*\n SYM_CONCEPT
^[Dd][Ee][Ff][Ii][Nn][Ii][Tt][Ii][Oo][Nn][ \t\r]*\n SYM_DEFINITION
-- mini-parser to match V_DADL_TEXT
^[Ll][Aa][Nn][Gg][Uu][Aa][Gg][Ee][ \t\r]*\n SYM_LANGUAGE
-- mini-parser to match V_DADL_TEXT
^[Dd][Ee][Ss][Cc][Rr][Ii][Pp][Tt][Ii][Oo][Nn][ \t\r]*\n SYM_DESCRIPTION
-- mini-parser to match V_CADL_TEXT
^[Ii][Nn][Vv][Aa][Rr][Ii][Aa][Nn][Tt][ \t\r]*\n SYM_INVARIANT
-- mini-parser to match V_ASSERTION_TEXT
^[Oo][Nn][Tt][Oo][Ll][Oo][Gg][Yy][ \t\r]*\n SYM_ONTOLOGY
-- mini-parser to match V_DADL_TEXT
----------/* V_DADL_TEXT */ -------------------------------------
<IN_DADL_SECTION>{
-- the following 2 patterns are a hack, until ADL2 comes into being;
-- until then, dADL blocks in an archetype finish when they
-- hit EOF, or else the 'description' or 'definition' keywords.
-- It's not nice, but it's simple ;-)
-- For both these patterns, the lexer has to unread what it
-- has just matched, store the dADL text so far, then get out
-- of the IN_DADL_SECTION state
^[Dd][Ee][Ff][Ii][Nn][Ii][Tt][Ii][Oo][Nn][ \t\r]*\n
^[Dd][Ee][Sc][Rr][Ii][Pp][Tt][Ii][Oo][Nn][ \t\r]*\n
[^\n]+\n -- any text on line with a LF
[^\n]+ -- any text on line with no LF
<<EOF>> -- (escape condition)
(.|\n) -- ignore unmatched chars
}
----------/* V_CADL_TEXT */ -------------------------------------
<IN_CADL_SECTION>{
^[ \t]+[^\n]*\n -- non-blank lines
\n+ -- blank lines
^[^ \t] -- non-white space at start (escape condition)
}
----------/* V_ASSERTION_TEXT */ -------------------------------------
<IN_ASSERTION_SECTION>{
^[ \t]+[^\n]*\n -- non-blank lines
^[^ \t] -- non-white space at start (escape condition)
}
----------/* V_VERSION_STRING */ -------------------------------------
[0-9]+\.[0-9]+(\.[0-9]+)*
----------/* V_LOCAL_TERM_CODE_REF */ --------------------------------------
\[[a-zA-Z0-9][a-zA-Z0-9.-]*\]
----------/* V_ARCHETYPE_ID */ ---------------------------------------------
[a-zA-Z][a-zA-Z0-9_]+(-[a-zA-Z][a-zA-Z0-9_]+){2}\.[a-zA-Z][a-zA-Z0-9_]+(-[azA-Z][a-zA-Z0-9_]+)*\.v[1-9][0-9]*
----------/* V_IDENTIFIER */ ----------------------------------------------
[a-zA-Z][a-zA-Z0-9_]*
9. Customising ADL
9.1. Introduction
Standard ADL has a completely regular way of representing constraints. Type names and attribute names from a reference model are mentioned in an alternating, hierarchical structure that is isomorphic to the aggregation structure of the corresponding classes in the reference model. Constraints at the leaf nodes are represented in a syntactic way that avoids committing to particular modelling details. The overall result enables constraints on most reference model types to be expressed. This section describes how to handle exceptions from the standard semantics. openEHR uses a small number of such exceptions, which are documented in the openEHR Archetype Profile (oAP) specification.
A situation in which standard ADL falls short is when the required semantics of constraint are different from those available naturally from the standard approach. Consider a reference model type QTY, shown in the following figure, which could be used to represent a person’s age in an archetype.

A typical ADL constraint to enable QTY to be used to represent age in clinical data can be expressed in natural language as follows:
property matches "time"
units matches "years" or "months"
if units is "years" then magnitude matches 0..200 (for adults)
if units is "months" then magnitude matches 3..36 (for infants)
The standard ADL expression for this requires the use of multiple alternatives, as follows:
age matches {
QTY matches {
property matches {"time"}
units matches {"yr"}
magnitude matches {|0.0..200.0|}
}
QTY matches {
property matches {"time"}
units matches {"mth"}
magnitude matches {|3.0..12.0|}
}
}While this is a perfectly legal approach, it is not the most natural expression of the required constraint, since it repeats the constraint of property matching "time". It also makes processing by software slightly more difficult than necessary.
A more convenient possibility is to introduce a new class into the archetype model, representing the concept "constraint on QTY", which we will call C_QTY. Such a class fits into the class model of archetypes (see the openEHR AOM) by inheriting from the class C_DOMAIN_TYPE. A C_QTY class is illustrated below, and corresponds to the way constraints on QTY objects are often expressed in user applications, which is to say, a property constraint, and a separate list of units/magnitude pairs.
The question now is how to express a constraint corresponding to this class in an ADL archetype. The solution is logical, and uses standard ADL. Consider that a particular constraint on a QTY must be an instance of the C_QTY type. An instance of any class can be expressed in ADL using the dADL sytnax (ADL’s object serialisation syntax) at the appropriate point in the archetype, as follows:
value matches {
C_QTY <
property = <"time">
list = <
["1"] = <
units = <"yr">
magnitude = <|0.0..200.0|>
>
["2"] = <
units = <"mth">
magnitude = <|1.0..36.0|>
>
>
>
}This approach can be used for any custom type which represents a constraint on a reference model type. Since the syntax is generic, only one change is needed to an ADL parser to support dADL sections within the cADL (definition) part of an archetype. The syntax rules are as follows:
-
the dADL section occurs inside the
{}block where its standard ADL equivalent would have occurred (i.e. no other delimiters or special marks are needed); -
the dADL section must be ‘typed’, i.e. it must start with a type name, which should correspond directly to a reference model type;
-
the dADL instance must obey the semantics of the custom type of which it is an instance, i.e. include the correct attribute names and relationships.
It should be understood of course, that just because a custom constraint type has been defined, it does not need to be used to express constraints on the reference model type it targets. Indeed, any mixture of standard ADL and dADL-expressed custom constraints may be used within the one archetype.
|
Note
|
that the classes in the above example are a simplified form of classes found in the openEHR reference model, designed purely for the purpose of the example. |
9.1.1. Custom Syntax
A dADL section is not the only possibility for expressing a custom constraint type. A useful alternative is a custom addition to the ADL syntax. Custom syntax can be smaller, more intuitive to read, and easier to parse than embedded dADL sections. A typical example of the use of custom syntax is to express constraints on the type CODE_PHRASE in the openEHR reference model (rm.data_types package). This type models the notion of a ‘coded term’, which is ubiquitous in clinical computing. The standard ADL for a constraint on the defining_code attribute of a class CODE_PHRASE is as follows:
defining_code matches {
CODE_PHRASE matches {
terminology_id matches {"local"}
code_string matches {"at0039"} -- lying
}
CODE_PHRASE matches {
terminology_id matches {"local"}
code_string matches {"at0040"} -- sitting
}
}However, as with QUANTITY, the most typical constraint required on a CODE_PHRASE is factored differently from the standard ADL - the need is almost always to specify the terminology, and then a set of code_strings. A type C_CODE_PHRASE type can be defined as shown in the figure below.
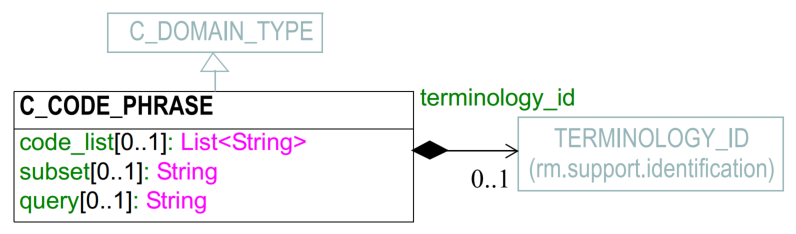
Using the dADL section method, including a C_CODE_PHRASE constraint would require the following section:
defining_code matches {
C_CODE_PHRASE <
terminology_id = <
value = <"local">
>
code_list = <
["1"] = <"at0039">
["2"] = <"at0040">
>
>
}Although this is perfectly legal, a more compact and readable rendition of this same constraint is provided by a custom syntax addition to ADL, which enables the above example to be written as follows:
defining_code matches {
[local::
at0039,
at0040]
}The above syntax should be understood as an extension to the ADL grammar, and an archetype tool supporting the extension needs to have a modified parser. While these two ADL fragments express exactly the same constraint, the second is shorter and clearer.
Appendix A: Relationship of ADL to Other Formalisms
A.1. Overview
Whenever a new formalism is defined, it is reasonable to ask the question: are there not existing formalisms which would do the same job? Research to date has shown that in fact, no other formalism has been designed for the same use, and none easily express ADL’s semantics. During ADL’s initial development, it was felt that there was great value in analysing the problem space very carefully, and constructing an abstract syntax exactly matched to the solution, rather than attempting to use some other formalism - undoubtedly designed for a different purpose - to try and express the semantics of archetypes, or worse, to start with an XML-based exchange format, which often leads to the conflation of abstract and concrete representational semantics. Instead, the approach used has paid off, in that the resulting syntax is very simple and powerful, and in fact has allowed mappings to other formalisms to be more correctly defined and understood. The following sections compare ADL to other formalisms and show how it is different.
A.2. Constraint Syntaxes
A.2.1. OMG OCL (Object Constraint Language)
The OMG’s Object Constraint Language (OCL) appears at first glance to be an obvious contender for writing archetypes. However, its designed use is to write constraints on object models, rather than on data, which is what archetypes are about. As a concrete example, OCL can be used to make statements about the actors attribute of a class Company - e.g. that actors must exist and contain the Actor who is the lead of Company. However, if used in the normal way to write constraints on a class model, it cannot describe the notion that for a particular kind of (acting) company, such as 'itinerant jugglers', there must be at least four actors, each of whom have among their capabilities 'advanced juggling', plus an Actor who has skill 'musician'. This is because doing so would constrain all instances of the class Company to conform to the specific configuration of instances corresponding to actors and jugglers, when what is intended is to allow a myriad of possibilities. ADL provides the ability to create numerous archetypes, each describing in detail a concrete configuration of instances of type Company. OCL’s constraint types include function pre- and post-conditions, and class invariants. There is no structural character to the syntax - all statements are essentially first-order predicate logic statements about elements in models expressed in UML, and are related to parts of a model by 'context' statements. This makes it impossible to use OCL to express an archetype in a structural way which is natural to domain experts. OCL also has some flaws, described by Beale [beale_ocl]. However, OCL is in fact relevant to ADL. ADL archetypes include invariants (and one day, might include pre- and post-conditions). Currently these are expressed in a syntax very similar to OCL, with minor differences. The exact definition of the ADL invariant syntax in the future will depend somewhat on the progress of OCL through the OMG standards process.
A.3. Ontology Formalisms
A.3.1. OWL (Web Ontology Language)
The W3C Web Ontology Language (OWL) is a W3C initiative for defining Web-enabled ontologies which aim to allow the building of the "Semantic Web". OWL has an abstract syntax, developed at the University of Manchester, UK, and an exchange syntax, which is an extension of the XML-based syntax known as RDF (Resource Description Framework). We discuss OWL only in terms of its abstract syntax, since this is a semantic representation of the language unencumbered by XML or RDF details (there are tools which convert between abstract OWL and various exchange syntaxes).
OWL is a general purpose description logic (DL), and is primarily used to describe 'classes' of things in such a way as to support subsumptive inferencing within the ontology, and by extension, on data which are instances of ontology classes. There is no general assumption that the data itself were built based on any particular class model - they might be audio-visual objects in an archive, technical documentation for an aircraft or the Web pages of a company. OWL’s class definitions are therefore usually constraint statements on an implied model on which data appear to be based. However, the semantics of an information model can themselves be represented in OWL. Restrictions are the primary way of defining subclasses.
In intention, OWL is aimed at representing some 'reality' and then making inferences about it; for example in a medical ontology, it can infer that a particular patient is at risk of ischemic heart disease due to smoking and high cholesterol, if the knowledge that 'ischemic heart disease has-risk-factor smoking' and 'ischemic heart disease has-risk-factor high cholesterol' are in the ontology, along with a representation of the patient details themselves. OWL’s inferencing works by subsumption, which is to say, asserting either that an 'individual' (OWL’s equivalent of an object-oriented instance or a type) conforms to a 'class', or that a particular 'class' 'is-a' (subtype of another) 'class'; this approach can also be understood as category-based reasoning or set-containment.
ADL can also be thought of as being aimed at describing a 'reality', and allowing inferences to be made. However, the reality it describes is in terms of constraints on information structures (based on an underlying information model), and the inferencing is between data and the constraints. Some of the differences between ADL and OWL are as follows.
-
ADL syntax is predicated on the existence of existing object-oriented reference models, expressed in UML or some similar formalism, and the constraints in an ADL archetype are in relation to types and attributes from such a model. In contrast, OWL is far more general, and requires the explicit expression of a reference model in OWL, before archetype-like constraints can be expressed.
-
Because information structures are in general hierarchical compositions of nodes and elements, and may be quite deep, ADL enables constraints to be expressed in a structural, nested way, mimicking the tree-like nature of the data it constrains. OWL does not provide a native way to do this, and although it is possible to express approximately the same constraints in OWL, it is fairly inconvenient, and would probably only be made easy by machine conversion from a visual format more or less like ADL.
-
As a natural consequence of dealing with heavily nested structures in a natural way, ADL also provides a path syntax, based on Xpath [owl_xpath], enabling any node in an archetype to be referenced by a path or path pattern. OWL does not provide an inbuilt path mechanism; Xpath can presumably be used with the RDF representation, although it is not yet clear how meaningful the paths would be with respect to the named categories within an OWL ontology.
-
ADL also natively takes care of disengaging natural language and terminology issues from constraint statements by having a separate ontology per archetype, which contains 'bindings' and language-specific translations. OWL has no inbuilt syntax for this, requiring such semantics to be represented from first principles.
-
ADL provides a rich set of constraints on primitive types, including dates and times. OWL 1.0 (c 2005) did not provide any equivalents; OWL 1.1 (c 2007) look as though it provides some.
Research to date shows that the semantics of an archetype are likely to be representable inside OWL, assuming expected changes to improve its primitive constraint types occur. To do so would require the following steps:
-
express the relevant reference models in OWL (this has been shown to be possible);
-
express the relevant terminologies in OWL (research on this is ongoing);
-
be able to represent concepts (i.e. constraints) independently of natural language (status unknown);
-
convert the cADL part of an archetype to OWL; assuming the problem of primitive type constraints is solved, research to date shows that this should in principle be possible.
To use the archetype on data, the data themselves would have to be converted to OWL, i.e. be expressed as 'individuals'. In conclusion, we can say that mathematical equivalence between OWL and ADL is probably provable. However, it is clear that OWL is far from a convenient formalism to express archetypes, or to use them for modelling or reasoning against data. The ADL approach makes use of existing UML semantics and existing terminologies, and adds a convenient syntax for expressing the required constraints. It also appears fairly clear that even if all of the above conversions were achieved, using OWL-expressed archetypes to validate data (which would require massive amounts of data to be converted to OWL statements) is unlikely to be anywhere near as efficient as doing it with archetypes expressed in ADL or one of its concrete expressions.
Nevertheless, OWL provides a very powerful generic reasoning framework, and offers a great deal of inferencing power of far wider scope than the specific kind of 'reasoning' provided by archetypes. It appears that it could be useful for the following archetype-related purposes:
-
providing access to ontological resources while authoring archetypes, including terminologies, pure domain-specific ontologies, etc;
-
providing a semantic 'indexing' mechanism allowing archetype authors to find archetypes relating to specific subjects (which might not be mentioned literally within the archetypes);
-
providing inferencing on archetypes in order to determine if a given archetype is subsumed within another archetype which it does not specialise (in the ADL sense);
-
providing access to archetypes from within a semantic Web environment, such as an ebXML server or similar.
A.3.2. KIF (Knowledge Interchange Format)
The Knowledge Interchange Format (KIF) is a knowledge representation language whose goal is to be able to describe formal semantics which would be sharable among software entities, such as information systems in an airline and a travel agency. An example of KIF (taken from [Gruber]) used to describe the simple concept of 'units' in a class is as follows:
(defrelation BASIC-UNIT
(=> (BASIC-UNIT ?u) ; basic units are distinguished units of measure
(unit-of-measure ?u)))
(deffunction UNIT*
; Unit* maps all pairs of units to units
(=> (and (unit-of-measure ?u1) (unit-of-measure ?u2))
(and (defined (UNIT* ?u1 ?u2)) (unit-of-measure (UNIT* ?u1 ?u2))))
; It is commutative
(= (UNIT* ?u1 ?u2) (UNIT* ?u2 ?u1))
; It is associative
(= (UNIT* ?u1 (UNIT* ?u2 ?u3))
(UNIT* (UNIT* ?u1 ?u2) ?u3))
)
(deffunction UNIT^
; Unit^ maps all units and reals to units
(=> (and (unit-of-measure ?u)
(real-number ?r))
(and (defined (UNIT^ ?u ?r)) (unit-of-measure (UNIT^ ?u ?r))))
; It has the algebraic properties of exponentiation
(= (UNIT^ ?u 1) ?u)
(= (unit* (UNIT^ ?u ?r1) (UNIT^ ?u ?r2)) (UNIT^ ?u (+ ?r1 ?r2)))
(= (UNIT^ (unit* ?u1 ?u2) ?r)
(unit* (UNIT^ ?u1 ?r) (UNIT^ ?u2 ?r)))
)It should be clear from the above that KIF is a definitional language - it defines all the concepts it mentions. However, the most common situation in which we find ourselves is that information models already exist, and may even have been deployed as software. Thus, to use KIF for expressing archetypes, the existing information model and relevant terminologies would have to be converted to KIF statements, before archetypes themselves could be expressed. This is essentially the same process as for expressing archetypes in OWL.
It should also be realised that KIF is intended as a knowledge exchange format, rather than a knowledge representation format, which is to say that it can (in theory) represent the semantics of any other knowledge representation language, such as OWL. This distinction today seems fine, since Web-enabled languages like OWL probably don’t need an exchange format other than their XML equivalents to be shared. The relationship and relative strengths and deficiencies is explored by e.g. [Martin].
A.4. XML-based Formalisms
A.4.1. XML-schema
Previously, archetypes have been expressed as XML instance documents conforming to W3C XML schemas, for example in the Good Electronic Health Record (see [GeHR_AUS] and openEHR projects. The schemas used in those projects correspond technically to the XML expressions of information model-dependent object models shown in The Archetypes: Technical Overview specification. XML archetypes are accordingly equivalent to serialised instances of the parse tree, i.e. particular ADL archetypes serialised from objects into XML instance.
Appendix B: Extended Meta-data Guide
This section documents the use of the description/other_details meta-data subsection of an ADL 1.4 archetype. The meta-data items described here correspond to requirements discovered since the publication of the ADL and AOM 1.4 standards, and are designed to enable forward compatibility with ADL/AOM 2.
They are divided into two groups. The first set consists of standardised items whose naming and rules should be followed, and which are intended to be implemented by any ADL 1.4 ⇒ ADL 2 conversion tool. The second set consists of items that have been used publicly by at least one organisation and should be considered either candidates for standardisation, or else as item names reserved from other use (i.e. to avoid future clashes).
Note that since the syntax structure of the other_details subsection is a Hash <String, String>, all values are just strings. However, some internal syntax rules are imposed or suggested to enable smart parsing to generate more complex structures. An example is the use of the typical string for a person or organisation of the form "name <URN>", which enables email addresses, website URLs etc to be easily extracted.
B.1. Standardised Items
The standard items are defined as follows:
| Item | String syntax | Description |
|---|---|---|
revision |
Full version identifier to compensate for only major version numbering in ADL 1.4 identifiers. |
|
build_uid |
Guid string |
Changed every save. See AOM2 spec, Machine Identifiers section |
original_namespace |
reverse domain name |
See AOM2 spec, Governance Meta-data section. |
original_publisher |
org name with optional trailing |
See AOM2 spec, Governance Meta-data section |
custodian_organisation |
org name with optional trailing |
See AOM2 spec, Governance Meta-data section |
custodian_namespace |
reverse domain name |
See AOM2 spec, Governance Meta-data section |
licence |
free string with optional trailing |
Licence under which this archetype is shared. |
references |
string with one LF ( |
Online or publication references relevant to the archetype. |
ip_acknowledgements |
string with one LF ( |
Copyright and trademark notices. |
The following provides an example:
other_details = <
["licence"] = <"This work is licensed under the Creative Commons Attribution-ShareAlike 3.0 License. To view a copy of this license, visit http://creativecommons.org/licenses/by-sa/3.0/.">
["original_namespace"] = <"au.gov.nehta">
["original_publisher"] = <"NEHTA CTI Team, National E-Health Transition Authority <clinicalinfo@nehta.gov.au>">
["custodian_organisation"] = <"openEHR Foundation <http://www.openEHR.org>">
["custodian_namespace"] = <"org.openehr">
["build_uid"] = <"3076af96-e1dd-4f9b-abf2-23913fcf52b1">
["revision"] = <"0.0.1-alpha">
["references"] = <"
O'Brien E, Asmar R, Beilin L, et al. European Society of Hypertension recommendations for conventional, ambulatory and home blood pressure measurement. Journal of Hypertension. 2003; 21(5):821-848. Available from: http://www.ncbi.nlm.nih.gov/pubmed/12714851
Perloff D, Grim C, Flack J, Frohlich ED, Hill M, McDonald M, Morgenstern BZ. Human blood pressure determination by sphygmomanometry. Circulation. 1993; 88(5):2460. Available from: http://circ.ahajournals.org/cgi/reprint/88/5/2460
">
["ip_acknowledgements"] = <"
Content from LOINC® is copyright © 1995 Regenstrief Institute, Inc. and the LOINC Committee, and available at no cost under the license at http://loinc.org/terms-of-use.
Content from SNOMED CT® is copyright © 2007 IHTSDO <ihtsdo.org>.
">
>B.2. Other Items
The 'other' category is documented below.
| Item | String syntax | Description |
|---|---|---|
MD5-CAM-1.0.1 |
MD5 32-bit hex number string |
Used by CKM and openEHR template tools. |
current_contact |
person name with optional trailing |
CKM does nothing with this, except display. |
review_date |
ISO 8601 compliant date string |
Indicate the next time the archetype should be reviewed. Used by CKM in display only. |
responsible_organisation |
org name with optional trailing |
The name of the responsible organisation may be different to the custodian organisation. Used by CKM in display only. |
The following provides an example:
other_details = <
["review_date"] = <"2014-06-10">
["current_contact"] = <"Ian McNicoll, freshEHR Clinical Informatics Ltd <ian.mcnicoll@freshehr.com>">
["responsible_organisation"] = <"Nehta">
["MD5-CAM-1.0.1"] = <"C5016B71B55DBDCBCAA8531CC1A982E3">
>Appendix C: Syntax Specification
The normative specification of the ADL1.4 syntax is expressed in Antlr4 as a series of component grammars, shown below. This has been tested with the Antlr 4.9 implementation available from Antlr.org. The source files are available in two locations on Github - adl-antlr repository. The ODIN grammar used in parts of an ADL archetype is not shown below, it can be found in the openEHR ODIN specification.
|
Note
|
this form of Antlr grammars is non-modal and mixed (i.e. parsers and lexers in same files). This will be changed in the next version to separated files and modal lexing, to deal better with ODIN embedded in ADL and related issues. |
C.1. ADL Outer Syntax
The following grammar expresses the outer syntax of ADL, i.e. the top-level structure of section keywords and initial identification lines in an ADL text.
//
// description: Antlr4 grammar for Archetype Definition Language (ADL2)
// author: Thomas Beale <thomas.beale@openehr.org>
// contributors:Pieter Bos <pieter.bos@nedap.com>
// support: openEHR Specifications PR tracker <https://openehr.atlassian.net/projects/SPECPR/issues>
// copyright: Copyright (c) 2015- openEHR Foundation <http://www.openEHR.org>
// license: Apache 2.0 License <http://www.apache.org/licenses/LICENSE-2.0.html>
//
grammar adl14;
import cadl14, odin;
//
// ============== Parser rules ==============
//
adl14_archetype: ( archetype) EOF ;
archetype:
SYM_ARCHETYPE meta_data?
ARCHETYPE_HRID
specialization_section?
concept_section
language_section
description_section
definition_section
invariant_section?
ontology_section
;
specialization_section : SYM_SPECIALIZE ARCHETYPE_REF ;
language_section : SYM_LANGUAGE odin_text ;
description_section : SYM_DESCRIPTION odin_text ;
definition_section : SYM_DEFINITION c_complex_object ;
invariant_section : SYM_INVARIANT ( statement (';')?)+ ;
ontology_section : SYM_ONTOLOGY odin_text ;
concept_section:
'concept' '[' AT_CODE ']';
meta_data: '(' meta_data_item (';' meta_data_item )* ')' ;
meta_data_item:
meta_data_tag_adl_version '=' VERSION_ID
| meta_data_tag_uid '=' GUID
| meta_data_tag_build_uid '=' GUID
| meta_data_tag_rm_release '=' VERSION_ID
| meta_data_tag_is_controlled
| meta_data_tag_is_generated
| ALPHANUM_ID ( '=' meta_data_value )?
;
meta_data_value:
primitive_value
| GUID
| VERSION_ID
;
meta_data_tag_adl_version : 'adl_version' ;
meta_data_tag_uid : 'uid' ;
meta_data_tag_build_uid : 'build_uid' ;
meta_data_tag_rm_release : 'rm_release' ;
meta_data_tag_is_controlled : 'controlled' ;
meta_data_tag_is_generated : 'generated' ;
//
// ------------------ lexical patterns -----------------
//
SYM_ARCHETYPE : [Aa][Rr][Cc][Hh][Ee][Tt][Yy][Pp][Ee] ;
SYM_SPECIALIZE : '\n'[Ss][Pp][Ee][Cc][Ii][Aa][Ll][Ii][SsZz][Ee] ;
SYM_LANGUAGE : '\n'[Ll][Aa][Nn][Gg][Uu][Aa][Gg][Ee] ;
SYM_DESCRIPTION : '\n'[Dd][Ee][Ss][Cc][Rr][Ii][Pp][Tt][Ii][Oo][Nn] ;
SYM_DEFINITION : '\n'[Dd][Ee][Ff][Ii][Nn][Ii][Tt][Ii][Oo][Nn] ;
SYM_INVARIANT : '\n'[Ii][Nn][Vv][Aa][Rr][Ii][Aa][Nn][Tt] ;
SYM_ONTOLOGY : '\n'[Oo][Nn][Tt][Oo][Ll][Oo][Gg][Yy] ;
SYM_ANNOTATIONS : '\n'[Aa][Nn][Nn][Oo][Tt][Aa][Tt][Ii][Oo][Nn][Ss] ;
// ---------------- meta-data keywords and symbols ---------------
SYM_EQ : '=' ;
ALPHANUM_ID : [a-zA-Z0-9][a-zA-Z0-9_]* ;C.2. cADL Syntax
The following grammar expresses the syntax of cADL composite types, i.e. the language of the definition section of an archetype.
//
// description: Antlr4 grammar for cADL non-primitves sub-syntax of Archetype Definition Language (ADL2)
// author: Thomas Beale <thomas.beale@openehr.org>
// contributors:Pieter Bos <pieter.bos@nedap.com>
// support: openEHR Specifications PR tracker <https://openehr.atlassian.net/projects/SPECPR/issues>
// copyright: Copyright (c) 2015- openEHR Foundation <http://www.openEHR.org>
// license: Apache 2.0 License <http://www.apache.org/licenses/LICENSE-2.0.html>
//
grammar cadl14;
import cadl14_primitives, odin, base_expressions;
//
// ======================= Top-level Objects ========================
//
c_complex_object: rm_type_id (at_type_id)? c_occurrences? ( SYM_MATCHES '{' (c_attribute+ | '*') '}' )? ;
at_type_id: '[' ( AT_CODE ) ']';
// ======================== Components =======================
c_objects: c_non_primitive_object_ordered+ | c_primitive_object ;
c_non_primitive_object_ordered: c_non_primitive_object ;
c_non_primitive_object:
c_complex_object
| domain_specific_extension
| c_archetype_root
| c_complex_object_proxy
| archetype_slot
| c_ordinal
;
domain_specific_extension: rm_type_id '<' odin_text? '>';
c_ordinal: ordinal_term (',' ordinal_term)* (';' assumed_ordinal_value)?;
assumed_ordinal_value: INTEGER | REAL;
ordinal_term: (integer_value | real_value) '|' c_terminology_code;
c_archetype_root: SYM_USE_ARCHETYPE rm_type_id '[' AT_CODE (',' ARCHETYPE_REF)? ']' c_occurrences? ( SYM_MATCHES '{' c_attribute+ '}' )? ;
c_complex_object_proxy: SYM_USE_NODE rm_type_id ('[' AT_CODE ']')? c_occurrences? ADL_PATH ;
archetype_slot:
c_archetype_slot_head SYM_MATCHES '{' c_includes? c_excludes? '}'
| c_archetype_slot_head
;
c_archetype_slot_head: c_archetype_slot_id c_occurrences? ;
c_archetype_slot_id: SYM_ALLOW_ARCHETYPE rm_type_id ('[' AT_CODE ']')? ;
c_attribute: rm_attribute_id c_existence? c_cardinality? ( SYM_MATCHES '{' (c_objects | '*') '}' )? ;
c_includes : SYM_INCLUDE assertion+ ;
c_excludes : SYM_EXCLUDE assertion+ ;
c_existence: SYM_EXISTENCE SYM_MATCHES '{' existence '}' ;
existence: INTEGER | INTEGER '..' INTEGER ;
c_cardinality : SYM_CARDINALITY SYM_MATCHES '{' cardinality '}' ;
cardinality : multiplicity ( multiplicity_mod multiplicity_mod? )? ; // max of two
ordering_mod : ';' ( SYM_ORDERED | SYM_UNORDERED ) ;
unique_mod : ';' SYM_UNIQUE ;
multiplicity_mod : ordering_mod | unique_mod ;
c_occurrences : SYM_OCCURRENCES SYM_MATCHES '{' multiplicity '}' ;
multiplicity : INTEGER | '*' | INTEGER '..' ( INTEGER | '*' ) ;
//
// ---------- Lexer patterns -----------------
//
// CADL keywords
SYM_EXISTENCE : [Ee][Xx][Ii][Ss][Tt][Ee][Nn][Cc][Ee] ;
SYM_OCCURRENCES : [Oo][Cc][Cc][Uu][Rr][Rr][Ee][Nn][Cc][Ee][Ss] ;
SYM_CARDINALITY : [Cc][Aa][Rr][Dd][Ii][Nn][Aa][Ll][Ii][Tt][Yy] ;
SYM_ORDERED : [Oo][Rr][Dd][Ee][Rr][Ee][Dd] ;
SYM_UNORDERED : [Uu][Nn][Oo][Rr][Dd][Ee][Rr][Ee][Dd] ;
SYM_UNIQUE : [Uu][Nn][Ii][Qq][Uu][Ee] ;
SYM_USE_NODE : [Uu][Ss][Ee][_][Nn][Oo][Dd][Ee] ;
SYM_USE_ARCHETYPE : [Uu][Ss][Ee][_][Aa][Rr][Cc][Hh][Ee][Tt][Yy][Pp][Ee] ;
SYM_ALLOW_ARCHETYPE : [Aa][Ll][Ll][Oo][Ww][_][Aa][Rr][Cc][Hh][Ee][Tt][Yy][Pp][Ee] ;
SYM_INCLUDE : [Ii][Nn][Cc][Ll][Uu][Dd][Ee] ;
SYM_EXCLUDE : [Ee][Xx][Cc][Ll][Uu][Dd][Ee] ;C.3. cADL Primitives Syntax
The following grammar defines the syntax of cADL primitives, which are used by cADL composites and also by ADL rules.
//
// description: Antlr4 grammar for cADL primitives sub-syntax of Archetype Definition Language (ADL2)
// author: Thomas Beale <thomas.beale@openehr.org>
// contributors:Pieter Bos <pieter.bos@nedap.com>
// support: openEHR Specifications PR tracker <https://openehr.atlassian.net/projects/SPECPR/issues>
// copyright: Copyright (c) 2015- openEHR Foundation <http://www.openEHR.org>
// license: Apache 2.0 License <http://www.apache.org/licenses/LICENSE-2.0.html>
//
grammar cadl14_primitives;
import odin_values;
//
// ======================= Parser rules ========================
//
c_primitive_object:
c_integer
| c_real
| c_date
| c_time
| c_date_time
| c_duration
| c_string
| c_terminology_code
| c_boolean
;
c_integer: ( integer_value | integer_list_value | integer_interval_value | integer_interval_list_value ) assumed_integer_value? ;
assumed_integer_value: ';' integer_value ;
c_real: ( real_value | real_list_value | real_interval_value | real_interval_list_value ) assumed_real_value? ;
assumed_real_value: ';' real_value ;
c_date_time: ( DATE_TIME_CONSTRAINT_PATTERN | date_time_value | date_time_list_value | date_time_interval_value | date_time_interval_list_value ) assumed_date_time_value? ;
assumed_date_time_value: ';' date_time_value ;
c_date: ( DATE_CONSTRAINT_PATTERN | date_value | date_list_value | date_interval_value | date_interval_list_value ) assumed_date_value? ;
assumed_date_value: ';' date_value ;
c_time: ( TIME_CONSTRAINT_PATTERN | time_value | time_list_value | time_interval_value | time_interval_list_value ) assumed_time_value? ;
assumed_time_value: ';' time_value ;
c_duration: (
DURATION_CONSTRAINT_PATTERN ( ( duration_interval_value | duration_value ))?
| duration_value | duration_list_value | duration_interval_value | duration_interval_list_value ) assumed_duration_value?
;
assumed_duration_value: ';' duration_value ;
c_string: ( string_value | string_list_value | regex_constraint ) assumed_string_value? ;
regex_constraint: SLASH_REGEX | CARET_REGEX ;
assumed_string_value: ';' string_value ;
c_terminology_code: c_local_term_code | c_qualified_term_code;
c_local_term_code: '[' ( ( AC_CODE ( ';' AT_CODE )? ) | AT_CODE ) ']' ;
//TERM_CODE_REF clashes a lot and is needed from within odin, unfortunately. Switching lexer modes might be better
c_qualified_term_code: '[' terminology_id '::' ( (terminology_code ( ',' terminology_code )* ';' terminology_code) )? ']' | TERM_CODE_REF;
terminology_id: ALPHA_LC_ID | ALPHA_UC_ID ;
terminology_code: AT_CODE | AC_CODE | ALPHA_LC_ID | ALPHA_UC_ID | INTEGER ;
c_boolean: ( boolean_value | boolean_list_value ) assumed_boolean_value? ;
assumed_boolean_value: ';' boolean_value ;
//
// ======================= Lexical rules ========================
//
// ---------- ISO8601-based date/time/duration constraint patterns
DATE_CONSTRAINT_PATTERN : YEAR_PATTERN '-' MONTH_PATTERN '-' DAY_PATTERN ;
TIME_CONSTRAINT_PATTERN : HOUR_PATTERN ':' MINUTE_PATTERN ':' SECOND_PATTERN ;
DATE_TIME_CONSTRAINT_PATTERN : DATE_CONSTRAINT_PATTERN 'T' TIME_CONSTRAINT_PATTERN ;
DURATION_CONSTRAINT_PATTERN : 'P' [yY]?[mM]?[Ww]?[dD]? ( 'T' [hH]?[mM]?[sS]? )? ('/')?;
// date time pattern
fragment YEAR_PATTERN : ( 'yyy' 'y'? ) | ( 'YYY' 'Y'? ) ;
fragment MONTH_PATTERN : 'mm' | 'MM' | '??' | 'XX' | 'xx' ;
fragment DAY_PATTERN : 'dd' | 'DD' | '??' | 'XX' | 'xx' ;
fragment HOUR_PATTERN : 'hh' | 'HH' | '??' | 'XX' | 'xx' ;
fragment MINUTE_PATTERN : 'mm' | 'MM' | '??' | 'XX' | 'xx' ;
fragment SECOND_PATTERN : 'ss' | 'SS' | '??' | 'XX' | 'xx' ;
// ---------- Delimited Regex matcher ------------
// In ADL, a regexp can only exist between {}.
// allows for '/' or '^' delimiters
// logical form - REGEX: '/' ( '\\/' | ~'/' )+ '/' | '^' ( '\\^' | ~'^' )+ '^';
// The following is used to ensure REGEXes don't get mixed up with paths, which use '/' chars
SLASH_REGEX: '/' SLASH_REGEX_CHAR+ '/';
fragment SLASH_REGEX_CHAR: ~[/\n\r] | ESCAPE_SEQ | '\\/';
CARET_REGEX: '^' CARET_REGEX_CHAR+ '^';
fragment CARET_REGEX_CHAR: ~[^\n\r] | ESCAPE_SEQ | '\\^';C.4. ADL Keywords
The following grammar defines the lexer patterns for ADL keywords.
//
// description: Antlr4 lexer grammar for keywords of Archetype Definition Language (ADL2)
// author: Thomas Beale <thomas.beale@openehr.org>
// support: openEHR Specifications PR tracker <https://openehr.atlassian.net/projects/SPECPR/issues>
// copyright: Copyright (c) 2015 openEHR Foundation
// license: Apache 2.0 License <http://www.apache.org/licenses/LICENSE-2.0.html>
//
lexer grammar adl_keywords;
// ADL keywords
SYM_ARCHETYPE : [Aa][Rr][Cc][Hh][Ee][Tt][Yy][Pp][Ee] ;
SYM_TEMPLATE : [Tt][Ee][Mm][Pp][Ll][Aa][Tt][Ee] ;
SYM_OPERATIONAL_TEMPLATE : [Oo][Pp][Ee][Rr][Aa][Tt][Ii][Oo][Nn][Aa][Ll]'_'[Tt][Ee][Mm][Pp][Ll][Aa][Tt][Ee] ;
SYM_SPECIALIZE : '\n'[Ss][Pp][Ee][Cc][Ii][Aa][Ll][Ii][SsZz][Ee] ;
SYM_LANGUAGE : '\n'[Ll][Aa][Nn][Gg][Uu][Aa][Gg][Ee] ;
SYM_DESCRIPTION : '\n'[Dd][Ee][Ss][Cc][Rr][Ii][Pp][Tt][Ii][Oo][Nn] ;
SYM_DEFINITION : '\n'[Dd][Ee][Ff][Ii][Nn][Ii][Tt][Ii][Oo][Nn] ;
SYM_RULES : '\n'[Rr][Uu][Ll][Ee][Ss] ;
SYM_TERMINOLOGY : '\n'[Tt][Ee][Rr][Mm][Ii][Nn][Oo][Ll][Oo][Gg][Yy] ;
SYM_ANNOTATIONS : '\n'[Aa][Nn][Nn][Oo][Tt][Aa][Tt][Ii][Oo][Nn][Ss] ;
SYM_COMPONENT_TERMINOLOGIES : '\n'[Cc][Oo][Mm][Pp][Oo][Nn][Ee][Nn][Tt]'_'[Tt][Ee][Rr][Mm][Ii][Nn][Oo][Ll][Oo][Gg][Ii][Ee][Ss] ;
// CADL keywords
SYM_EXISTENCE : [Ee][Xx][Ii][Ss][Tt][Ee][Nn][Cc][Ee] ;
SYM_OCCURRENCES : [Oo][Cc][Cc][Uu][Rr][Rr][Ee][Nn][Cc][Ee][Ss] ;
SYM_CARDINALITY : [Cc][Aa][Rr][Dd][Ii][Nn][Aa][Ll][Ii][Tt][Yy] ;
SYM_ORDERED : [Oo][Rr][Dd][Ee][Rr][Ee][Dd] ;
SYM_UNORDERED : [Uu][Nn][Oo][Rr][Dd][Ee][Rr][Ee][Dd] ;
SYM_UNIQUE : [Uu][Nn][Ii][Qq][Uu][Ee] ;
SYM_USE_NODE : [Uu][Ss][Ee][_][Nn][Oo][Dd][Ee] ;
SYM_USE_ARCHETYPE : [Uu][Ss][Ee][_][Aa][Rr][Cc][Hh][Ee][Tt][Yy][Pp][Ee] ;
SYM_ALLOW_ARCHETYPE : [Aa][Ll][Ll][Oo][Ww][_][Aa][Rr][Cc][Hh][Ee][Tt][Yy][Pp][Ee] ;
SYM_INCLUDE : [Ii][Nn][Cc][Ll][Uu][Dd][Ee] ;
SYM_EXCLUDE : [Ee][Xx][Cc][Ll][Uu][Dd][Ee] ;
SYM_AFTER : [Aa][Ff][Tt][Ee][Rr] ;
SYM_BEFORE : [Bb][Ee][Ff][Oo][Rr][Ee] ;
SYM_CLOSED : [Cc][Ll][Oo][Ss][Ee][Dd] ;
SYM_DEFAULT : '_' [Dd] [Ee] [Ff] [Aa] [Uu] [Ll] [Tt] ;
SYM_THEN : [Tt][Hh][Ee][Nn] ;
SYM_AND : [Aa][Nn][Dd] | '∧';
SYM_OR : [Oo][Rr] | '∨' ;
SYM_XOR : [Xx][Oo][Rr] ;
SYM_NOT : [Nn][Oo][Tt] | '!' | '∼' | '~' | '¬';
SYM_IMPLIES : [Ii][Mm][Pp][Ll][Ii][Ee][Ss] | '®';
SYM_FOR_ALL : [Ff][Oo][Rr][_][Aa][Ll][Ll] | '∀';
SYM_EXISTS : [Ee][Xx][Ii][Ss][Tt][Ss];
SYM_THERE_EXISTS: 'there_exists' | '∃' ;
SYM_MATCHES : [Mm][Aa][Tt][Cc][Hh][Ee][Ss] | [Ii][Ss]'_'[Ii][Nn] | '∈';C.5. Base Expressions
The following grammar defines syntax of expressions.
//
// description: Antlr4 grammar for openEHR Rules core syntax.
// author: Thomas Beale <thomas.beale@openehr.org>
// contributors:Pieter Bos <pieter.bos@nedap.com>
// support: openEHR Specifications PR tracker <https://openehr.atlassian.net/projects/SPECPR/issues>
// copyright: Copyright (c) 2016- openEHR Foundation <http://www.openEHR.org>
// license: Apache 2.0 License <http://www.apache.org/licenses/LICENSE-2.0.html>
//
grammar base_expressions;
import cadl2_primitives, odin_values;
//
// ======================= Top-level _objects ========================
//
statement_block: statement+ ;
// ------------------------- statements ---------------------------
statement: declaration | assignment | assertion;
declaration:
variable_declaration
| constant_declaration
;
variable_declaration: local_variable ':' type_id ( SYM_ASSIGNMENT expression )? ;
constant_declaration: constant_name ':' type_id ( SYM_EQ primitive_object )? ;
assignment:
binding
| local_assignment
;
//
// The following is the means of binding a data context path to a local variable
// TODO: remove this rule when proper external bindings are supported
binding: local_variable SYM_ASSIGNMENT bound_path ;
local_assignment: local_variable SYM_ASSIGNMENT expression ;
assertion: ( ( ALPHA_LC_ID | ALPHA_UC_ID ) ':' )? boolean_expr ;
//
// -------------------------- _expressions --------------------------
//
expression:
boolean_expr
| arithmetic_expr
;
//
// _expressions evaluating to boolean values, using standard precedence
// The equality_binop ones are not strictly necessary, but allow the use
// of boolean_leaf = true, which some people like
//
boolean_expr:
SYM_NOT boolean_expr
| boolean_expr SYM_AND boolean_expr
| boolean_expr SYM_XOR boolean_expr
| boolean_expr SYM_OR boolean_expr
| boolean_expr SYM_IMPLIES boolean_expr
| boolean_leaf equality_binop boolean_leaf
| boolean_leaf
;
//
// Atomic Boolean-valued expression elements
// TODO: SYM_EXISTS alternative to be replaced by defined() predicate
boolean_leaf:
boolean_literal
| for_all_expr
| there_exists_expr
| SYM_EXISTS ( bound_path | sub_path_local_variable )
| '(' boolean_expr ')'
| relational_expr
| equality_expr
| constraint_expr
| value_ref
;
boolean_literal:
SYM_TRUE
| SYM_FALSE
;
//
// Universal and existential quantifier
// TODO: 'in' probably isn't needed in the long term
for_all_expr: SYM_FOR_ALL VARIABLE_ID ( ':' | 'in' ) value_ref '|'? boolean_expr ;
there_exists_expr: SYM_THERE_EXISTS VARIABLE_ID ( ':' | 'in' ) value_ref '|'? boolean_expr ;
// Constraint expressions
// This provides a way of using one operator (matches) to compare a
// value (LHS) with a value range (RHS). As per ADL, the value range
// for ordered types like Integer, Date etc may be a single value,
// a list of values, or a list of intervals, and in future, potentially
// other comparators, including functions (e.g. divisible_by_N).
//
// For non-ordered types like String and Terminology_code, the RHS
// is in other forms, e.g. regex for Strings.
//
// The matches operator can be used to generate a Boolean value that
// may be used within an expression like any other Boolean (hence it
// is a booleanLeaf).
// TODO: non-primitive objects might be supported on the RHS in future.
constraint_expr: ( arithmetic_expr | value_ref ) SYM_MATCHES ( '{' c_inline_primitive_object '}' | CONTAINED_REGEXP );
//
// _expressions evaluating to arithmetic values, using standard precedence
//
arithmetic_expr:
<assoc=right> arithmetic_expr '^' arithmetic_expr
| arithmetic_expr ( '/' | '*' | '%' ) arithmetic_expr
| arithmetic_expr ( '+' | '-' ) arithmetic_expr
| arithmetic_leaf
;
arithmetic_leaf:
integer_value
| real_value
| date_value
| date_time_value
| time_value
| duration_value
| value_ref
| '(' arithmetic_expr ')'
;
//
// Equality expression between any arithmetic value; precedence is
// lowest, so only needed between leaves, since () will be needed for
// larger expressions anyway
//
equality_expr: arithmetic_expr equality_binop arithmetic_expr ;
equality_binop:
SYM_EQ
| SYM_NE
;
//
// Relational expressions of arithmetic operands generating Boolean values
//
relational_expr: arithmetic_expr relational_binop arithmetic_expr ;
relational_binop:
SYM_GT
| SYM_LT
| SYM_LE
| SYM_GE
;
//
// instances references: data references, variables, and function calls.
// TODO: Remove bound_path from this rule when external binding supported
//
value_ref:
function_call
| bound_path
| sub_path_local_variable
| local_variable
| constant_name
;
local_variable: VARIABLE_ID ;
// TODO: change to [] form, e.g. book_list [{title.contains("Quixote")}]
sub_path_local_variable: VARIABLE_WITH_PATH;
// TODO: Remove this rule when external binding supported
bound_path: ADL_PATH ;
constant_name: ALPHA_UC_ID ;
function_call: ALPHA_LC_ID '(' function_args? ')' ;
function_args: expression ( ',' expression )* ;
type_id: ALPHA_UC_ID ( '<' type_id ( ',' type_id )* '>' )? ;C.6. Base Lexer
The following grammar defines common lexical entities.
//
// General purpose patterns used in all openEHR parser and lexer tools
// author: Pieter Bos <pieter.bos@nedap.com>
// support: openEHR Specifications PR tracker <https://openehr.atlassian.net/projects/SPECPR/issues>
// copyright: Copyright (c) 2018- openEHR Foundation <http://www.openEHR.org>
//
lexer grammar base_lexer;
// ---------- whitespace & comments ----------
WS : [ \t\r]+ -> channel(HIDDEN) ;
LINE : '\r'? EOL -> channel(HIDDEN) ; // increment line count
CMT_LINE : '--' .*? '\r'? EOL -> skip ; // (increment line count)
fragment EOL : '\n' ;
// -------------- template overlay cannot be handled in a more simple way because it includes the comment line
SYM_TEMPLATE_OVERLAY : H_CMT_LINE (WS|LINE)* SYM_TEMPLATE_OVERLAY_ONLY;
fragment H_CMT_LINE : '--------' '-'*? ('\n'|'\r''\n'|'\r') ; // special type of comment for splitting template overlays
fragment SYM_TEMPLATE_OVERLAY_ONLY : [Tt][Ee][Mm][Pp][Ll][Aa][Tt][Ee]'_'[Oo][Vv][Ee][Rr][Ll][Aa][Yy] ;
// ---------- path patterns -----------
ADL_PATH : ADL_ABSOLUTE_PATH | ADL_RELATIVE_PATH;
fragment ADL_ABSOLUTE_PATH : ('/' ADL_PATH_SEGMENT)+;
fragment ADL_RELATIVE_PATH : ADL_PATH_SEGMENT ('/' ADL_PATH_SEGMENT)+;
fragment ADL_PATH_SEGMENT : ALPHA_LC_ID ('[' ADL_PATH_ATTRIBUTE ']')?;
fragment ADL_PATH_ATTRIBUTE : ID_CODE | STRING | INTEGER | ARCHETYPE_REF | ARCHETYPE_HRID;
// ---------- ISO8601-based date/time/duration constraint patterns
DATE_CONSTRAINT_PATTERN : YEAR_PATTERN '-' MONTH_PATTERN '-' DAY_PATTERN ;
TIME_CONSTRAINT_PATTERN : HOUR_PATTERN ':' MINUTE_PATTERN ':' SECOND_PATTERN ;
DATE_TIME_CONSTRAINT_PATTERN : DATE_CONSTRAINT_PATTERN 'T' TIME_CONSTRAINT_PATTERN ;
DURATION_CONSTRAINT_PATTERN : 'P' [yY]?[mM]?[Ww]?[dD]? ( 'T' [hH]?[mM]?[sS]? )? ;
// date time pattern
fragment YEAR_PATTERN : ( 'yyy' 'y'? ) | ( 'YYY' 'Y'? ) ;
fragment MONTH_PATTERN : 'mm' | 'MM' | '??' | 'XX' | 'xx' ;
fragment DAY_PATTERN : 'dd' | 'DD' | '??' | 'XX' | 'xx' ;
fragment HOUR_PATTERN : 'hh' | 'HH' | '??' | 'XX' | 'xx' ;
fragment MINUTE_PATTERN : 'mm' | 'MM' | '??' | 'XX' | 'xx' ;
fragment SECOND_PATTERN : 'ss' | 'SS' | '??' | 'XX' | 'xx' ;
// ---------- Delimited Regex matcher ------------
// In ADL, a regexp can only exist between {}.
// allows for '/' or '^' delimiters
// logical form - REGEX: '/' ( '\\/' | ~'/' )+ '/' | '^' ( '\\^' | ~'^' )+ '^';
// The following is used to ensure REGEXes don't get mixed up with paths, which use '/' chars
//a
// regexp can only exist between {}. It can optionally have an assumed value, by adding ;"value"
CONTAINED_REGEXP: '{'WS* (SLASH_REGEXP | CARET_REGEXP) WS* (';' WS* STRING)? WS* '}';
fragment SLASH_REGEXP: '/' SLASH_REGEXP_CHAR+ '/';
fragment SLASH_REGEXP_CHAR: ~[/\n\r] | ESCAPE_SEQ | '\\/';
fragment CARET_REGEXP: '^' CARET_REGEXP_CHAR+ '^';
fragment CARET_REGEXP_CHAR: ~[^\n\r] | ESCAPE_SEQ | '\\^';
// ---------- various ADL2 codes -------
ROOT_ID_CODE : 'id1' '.1'* ;
ID_CODE : 'id' CODE_STR ;
AT_CODE : 'at' CODE_STR ;
AC_CODE : 'ac' CODE_STR ;
fragment CODE_STR : ('0' | [1-9][0-9]*) ( '.' ('0' | [1-9][0-9]* ))* ;
// ---------- ISO8601 Date/Time values ----------
ISO8601_DATE : YEAR '-' MONTH ( '-' DAY )? | YEAR '-' MONTH '-' UNKNOWN_DT | YEAR '-' UNKNOWN_DT '-' UNKNOWN_DT ;
ISO8601_TIME : ( HOUR ':' MINUTE ( ':' SECOND ( SECOND_DEC_SEP DIGIT+ )?)? | HOUR ':' MINUTE ':' UNKNOWN_DT | HOUR ':' UNKNOWN_DT ':' UNKNOWN_DT ) TIMEZONE? ;
ISO8601_DATE_TIME : ( YEAR '-' MONTH '-' DAY 'T' HOUR (':' MINUTE (':' SECOND ( SECOND_DEC_SEP DIGIT+ )?)?)? | YEAR '-' MONTH '-' DAY 'T' HOUR ':' MINUTE ':' UNKNOWN_DT | YEAR '-' MONTH '-' DAY 'T' HOUR ':' UNKNOWN_DT ':' UNKNOWN_DT ) TIMEZONE? ;
fragment TIMEZONE : 'Z' | ('+'|'-') HOUR_MIN ; // hour offset, e.g. `+0930`, or else literal `Z` indicating +0000.
fragment YEAR : [0-9][0-9][0-9][0-9] ; // Year in ISO8601:2004 is 4 digits with 0-filling as needed
fragment MONTH : ( [0][1-9] | [1][0-2] ) ; // month in year
fragment DAY : ( [0][1-9] | [12][0-9] | [3][0-1] ) ; // day in month
fragment HOUR : ( [01]?[0-9] | [2][0-3] ) ; // hour in 24 hour clock
fragment MINUTE : [0-5][0-9] ; // minutes
fragment HOUR_MIN : ( [01]?[0-9] | [2][0-3] ) [0-5][0-9] ; // hour / minutes quad digit pattern
fragment SECOND : [0-5][0-9] ; // seconds
fragment SECOND_DEC_SEP : '.' | ',' ;
fragment UNKNOWN_DT : '??' ; // any unknown date/time value, except years.
// ISO8601 DURATION PnYnMnWnDTnnHnnMnn.nnnS
// here we allow a deviation from the standard to allow weeks to be // mixed in with the rest since this commonly occurs in medicine
// TODO: the following will incorrectly match just 'P'
ISO8601_DURATION : '-'?'P' (DIGIT+ [yY])? (DIGIT+ [mM])? (DIGIT+ [wW])? (DIGIT+[dD])? ('T' (DIGIT+[hH])? (DIGIT+[mM])? (DIGIT+ (SECOND_DEC_SEP DIGIT+)?[sS])?)? ;
// ------------------- special word symbols --------------
SYM_TRUE : [Tt][Rr][Uu][Ee] ;
SYM_FALSE : [Ff][Aa][Ll][Ss][Ee] ;
// ---------------------- Identifiers ---------------------
ARCHETYPE_HRID : ARCHETYPE_HRID_ROOT '.v' ARCHETYPE_VERSION_ID ;
ARCHETYPE_REF : ARCHETYPE_HRID_ROOT '.v' INTEGER ( '.' DIGIT+ )* ;
fragment ARCHETYPE_HRID_ROOT : (NAMESPACE '::')? IDENTIFIER '-' IDENTIFIER '-' IDENTIFIER '.' LABEL ;
fragment ARCHETYPE_VERSION_ID: DIGIT+ ('.' DIGIT+ ('.' DIGIT+ ( ( '-rc' | '-alpha' ) ( '.' DIGIT+ )? )?)?)? ;
VERSION_ID : DIGIT+ '.' DIGIT+ '.' DIGIT+ ( ( '-rc' | '-alpha' ) ( '.' DIGIT+ )? )? ;
fragment IDENTIFIER : ALPHA_CHAR WORD_CHAR* ;
// --------------------- composed primitive types -------------------
// e.g. [ICD10AM(1998)::F23]; [ISO_639-1::en]
TERM_CODE_REF : '[' TERM_CODE_CHAR+ ( '(' TERM_CODE_CHAR+ ')' )? '::' TERM_CODE_CHAR+ ']' ;
fragment TERM_CODE_CHAR: NAME_CHAR | '.';
// --------------------- URIs --------------------
// URI recogniser based on https://tools.ietf.org/html/rfc3986 and
// http://www.w3.org/Addressing/URL/5_URI_BNF.html
EMBEDDED_URI: '<' ([ \t\r\n]|CMT_LINE)* URI ([ \t\r\n]|CMT_LINE)* '>';
fragment URI : URI_SCHEME ':' URI_HIER_PART ( '?' URI_QUERY )? ('#' URI_FRAGMENT)? ;
fragment URI_HIER_PART : ( '//' URI_AUTHORITY ) URI_PATH_ABEMPTY
| URI_PATH_ABSOLUTE
| URI_PATH_ROOTLESS
| URI_PATH_EMPTY;
fragment URI_SCHEME : ALPHA_CHAR ( ALPHA_CHAR | DIGIT | '+' | '-' | '.')* ;
fragment URI_AUTHORITY : ( URI_USERINFO '@' )? URI_HOST ( ':' URI_PORT )? ;
fragment URI_USERINFO: (URI_UNRESERVED | URI_PCT_ENCODED | URI_SUB_DELIMS | ':' )* ;
fragment URI_HOST : URI_IP_LITERAL | URI_IPV4_ADDRESS | URI_REG_NAME ; //TODO: ipv6
fragment URI_PORT: DIGIT*;
fragment URI_IP_LITERAL : '[' URI_IPV6_LITERAL ']'; //TODO, if needed: IPvFuture
fragment URI_IPV4_ADDRESS : URI_DEC_OCTET '.' URI_DEC_OCTET '.' URI_DEC_OCTET '.' URI_DEC_OCTET ;
fragment URI_IPV6_LITERAL : HEX_QUAD (':' HEX_QUAD )* ':' ':' HEX_QUAD (':' HEX_QUAD )* ;
fragment URI_DEC_OCTET : DIGIT | [1-9] DIGIT | '1' DIGIT DIGIT | '2' [0-4] DIGIT | '25' [0-5];
fragment URI_REG_NAME: (URI_UNRESERVED | URI_PCT_ENCODED | URI_SUB_DELIMS)*;
fragment HEX_QUAD : HEX_DIGIT HEX_DIGIT HEX_DIGIT HEX_DIGIT ;
fragment URI_PATH_ABEMPTY: ('/' URI_SEGMENT ) *;
fragment URI_PATH_ABSOLUTE: '/' ( URI_SEGMENT_NZ ( '/' URI_SEGMENT )* )?;
fragment URI_PATH_NOSCHEME: URI_SEGMENT_NZ_NC ( '/' URI_SEGMENT )*;
fragment URI_PATH_ROOTLESS: URI_SEGMENT_NZ ( '/' URI_SEGMENT )*;
fragment URI_PATH_EMPTY: ;
fragment URI_SEGMENT: URI_PCHAR*;
fragment URI_SEGMENT_NZ: URI_PCHAR+;
fragment URI_SEGMENT_NZ_NC: ( URI_UNRESERVED | URI_PCT_ENCODED | URI_SUB_DELIMS | '@' )+; //non-zero-length segment without any colon ":"
fragment URI_PCHAR: URI_UNRESERVED | URI_PCT_ENCODED | URI_SUB_DELIMS | ':' | '@';
//fragment URI_PATH : '/' | ( '/' URI_XPALPHA+ )+ ('/')?;
fragment URI_QUERY : (URI_PCHAR | '/' | '?')*;
fragment URI_FRAGMENT : (URI_PCHAR | '/' | '?')*;
fragment URI_PCT_ENCODED : '%' HEX_DIGIT HEX_DIGIT ;
fragment URI_UNRESERVED: ALPHA_CHAR | DIGIT | '-' | '.' | '_' | '~';
fragment URI_RESERVED: URI_GEN_DELIMS | URI_SUB_DELIMS;
fragment URI_GEN_DELIMS: ':' | '/' | '?' | '#' | '[' | ']' | '@'; //TODO: migrate to [/?#...] notation
fragment URI_SUB_DELIMS: '!' | '$' | '&' | '\'' | '(' | ')'
| '*' | '+' | ',' | ';' | '=';
// According to IETF http://tools.ietf.org/html/rfc1034[RFC 1034] and http://tools.ietf.org/html/rfc1035[RFC 1035],
// as clarified by http://tools.ietf.org/html/rfc2181[RFC 2181] (section 11)
fragment NAMESPACE : LABEL ('.' LABEL)* ;
fragment LABEL : ALPHA_CHAR (NAME_CHAR|URI_PCT_ENCODED)* ;
GUID : HEX_DIGIT+ '-' HEX_DIGIT+ '-' HEX_DIGIT+ '-' HEX_DIGIT+ '-' HEX_DIGIT+ ;
ALPHA_UC_ID : ALPHA_UCHAR WORD_CHAR* ; // used for type ids
ALPHA_LC_ID : ALPHA_LCHAR WORD_CHAR* ; // used for attribute / method ids
ALPHA_UNDERSCORE_ID : '_' WORD_CHAR* ; // usually used for meta-model ids
// --------------------- atomic primitive types -------------------
INTEGER : DIGIT+ E_SUFFIX? ;
REAL : DIGIT+ '.' DIGIT+ E_SUFFIX? ;
fragment E_SUFFIX : [eE][+-]? DIGIT+ ;
STRING : '"' STRING_CHAR*? '"' ;
fragment STRING_CHAR : ~["\\] | ESCAPE_SEQ | UTF8CHAR ; // strings can be multi-line
CHARACTER : '\'' CHAR '\'' ;
fragment CHAR : ~['\\\r\n] | ESCAPE_SEQ | UTF8CHAR ;
fragment ESCAPE_SEQ: '\\' ['"?abfnrtv\\] ;
// ------------------- character fragments ------------------
fragment NAME_CHAR : WORD_CHAR | '-' ;
fragment WORD_CHAR : ALPHANUM_CHAR | '_' ;
fragment ALPHANUM_CHAR : ALPHA_CHAR | DIGIT ;
fragment ALPHA_CHAR : [a-zA-Z] ;
fragment ALPHA_UCHAR : [A-Z] ;
fragment ALPHA_LCHAR : [a-z] ;
fragment UTF8CHAR : '\\u' HEX_DIGIT HEX_DIGIT HEX_DIGIT HEX_DIGIT ;
fragment DIGIT : [0-9] ;
fragment HEX_DIGIT : [0-9a-fA-F] ;
// -------------------- common symbols ---------------------
SYM_COMMA: ',' ;
SYM_SEMI_COLON : ';' ;
SYM_LPAREN : '(';
SYM_RPAREN : ')';
SYM_LBRACKET : '[';
SYM_RBRACKET : ']';
SYM_LCURLY : '{' ;
SYM_RCURLY : '}' ;
// --------- symbols ----------
SYM_ASSIGNMENT: ':=' | '::=' ;
SYM_NE : '/=' | '!=' | '≠' ;
SYM_EQ : '=' ;
SYM_GT : '>' ;
SYM_LT : '<' ;
SYM_LE : '<=' | '≤' ;
SYM_GE : '>=' | '≥' ;
// TODO: remove when [] path predicates supported
VARIABLE_WITH_PATH: VARIABLE_ID ADL_ABSOLUTE_PATH ;
VARIABLE_ID: '$' ALPHA_LC_ID ;
//
// ========================= Lexer ============================
//
// -------------------- symbols for lists ------------------------
SYM_LIST_CONTINUE: '...' ;
// ------------------ symbols for intervals ----------------------
SYM_PLUS : '+' ;
SYM_MINUS : '-' ;
SYM_PLUS_OR_MINUS : '+/-' | '±' ;
SYM_PERCENT : '%' ;
SYM_CARAT: '^' ;
SYM_IVL_DELIM: '|' ;
SYM_IVL_SEP : '..' ;